Deep Reinforcement. .
En este proyecto se implementarán tres modelos de DRL en un mismo entorno, con el objetivo de analizar distintas formas de aprendizaje de un agente y estudiar su rendimiento. El agente será entrenado con los métodos:
- DQN doble (DDQN)
- Dueling DQN
- REINFORCE con línea de base
Contexto
Uno de los objetivos más actuales del campo de la robótica es conseguir que un robot sea capaz de aprender a realizar una serie de acciones por si sólo, del mismo modo que lo hace un niño pequeño. Esta es, básicamente, una de las principales motivaciones del aprendizaje por refuerzo profundo. Para ello se necesitan sistemas de control eficientes, especialmente para tareas complejas como pueden ser un despegue o un aterrizaje propio de drones autónomos y cohetes espaciales, y de un posible futuro transporte urbano, o de los cohetes espaciales reutilizables.
Con esta idea, usaremos un entorno ya predefinido en OpenAI, el Lunar Lander.
Lunar Lander consiste en una nave espacial que debe aterrizar en un lugar determinado del campo de observación. El agente conduce la nave y su objetivo es conseguir aterrizar en la pista de aterrizaje, coordenadas (0,0), y llegar con velocidad 0 (es decir, no debe estamparse contra el suelo). La nave consta de tres motores (izquierda, derecha y el principal que tiene debajo) que le permiten ir corrigiendo su rumbo hasta llegar a destino.
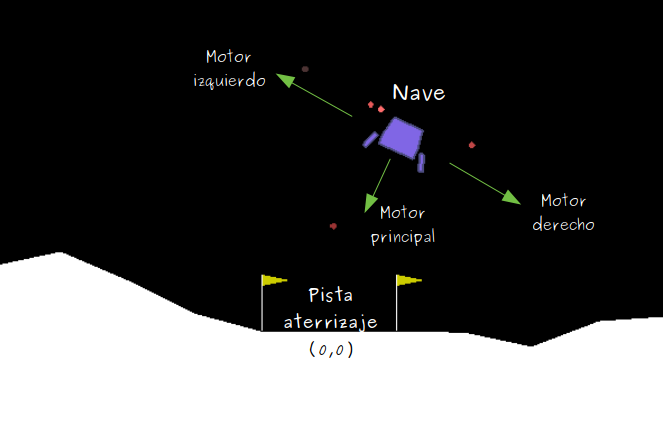
Las acciones que puede realizar la nave (espacio de acciones) son discretas y se categorizan según:
- 0 : No hacer nada
- 1 : Encender motor izquierdo
- 2 : Encender motor principal
- 3 : Encender motor derecho
Las recompensas obtenidas a lo largo del proceso de aterrizaje dependen de las acciones que se toman y del resultado que se deriva de ellas. Así:
- Desplazarse de arriba a abajo, hasta la zona de aterrizaje puede resultar en +100...+140 puntos
- Si se estrella, pierde -100 puntos
- Si consigue aterrizar en la zona de aterrizaje (velocidad 0), gana +100 puntos
- Si aterriza pero no en la zona de aterrizaje (fuera de las banderas amarillas) se pierden puntos
- El contacto de una pata con el suelo recibe +10 puntos (si se pierde contacto después de aterrizar, se pierden puntos)
- Cada vez que enciende el motor principal pierde -0.3 puntos
- Cada vez que enciende uno de los motores de izquierda o derecha, pierde -0.03 puntos
Para más detalles sobre la definición del entorno de Lunar Lander, se recomienda consultar el código fuente: https://github.com/openai/gym/blob/master/gym/envs/box2d/lunar_lander.py
La solución óptima es aquella en la que el agente, con un desplazamiento eficiente, consigue aterrizar en la zona de aterrizaje (0,0), tocando con las dos patas en el suelo y con velocidad nula. Se considera que el agente ha aprendido a realizar la tarea (i.e. el "juego" termina) cuando obtiene una media de almenos 200 puntos durante 100 episodios consecutivos.
Inicialización y exploración del entorno
IMPORTANTE: el entorno Lunar Lander requiere de la librería box2d-py:
- En local: instalar
conda install swigy luegopip install box2d-pydesde la terminal - En Google Colab: iniciar siempre notebook con
!pip install box2d-py
Empezaremos cargando las principales librerías necesarias para la práctica:
import gym
import matplotlib.pyplot as plt
%matplotlib inline
!pip install box2d-py
!pip install torch
import torch
import numpy as np
import io
import time
Requirement already satisfied: box2d-py in /Users/rubenperezibanez/.virtualenvs/openia/lib/python3.8/site-packages You are using pip version 9.0.1, however version 20.3.1 is available. You should consider upgrading via the 'pip install --upgrade pip' command. Requirement already satisfied: torch in /Users/rubenperezibanez/.virtualenvs/openia/lib/python3.8/site-packages Requirement already satisfied: numpy in /Users/rubenperezibanez/.virtualenvs/openia/lib/python3.8/site-packages (from torch) Requirement already satisfied: future in /Users/rubenperezibanez/.virtualenvs/openia/lib/python3.8/site-packages (from torch) Requirement already satisfied: typing-extensions in /Users/rubenperezibanez/.virtualenvs/openia/lib/python3.8/site-packages (from torch) Requirement already satisfied: dataclasses in /Users/rubenperezibanez/.virtualenvs/openia/lib/python3.8/site-packages (from torch) You are using pip version 9.0.1, however version 20.3.1 is available. You should consider upgrading via the 'pip install --upgrade pip' command.
Inicializar el entorno 'Lunar-Lander-v2'. Extraer el valor del umbral de recompensa definido en el entorno, el rango de recompensas permitido, el máximo de pasos establecidos por cada episodio, la dimensión del espacio de acciones, y la dimensión del espacio de observación.
env = gym.make('LunarLander-v2')
print("Action space is {
} ".format(env.action_space))
print("Observation space is {} ".format(env.observation_space))
print("Reward range is {
} ".format(env.reward_range))
obs = env.reset()
print("Obs inicial: {
} ".format(obs))
print("Máximo de pasos establecidos por cada episodio es {}".format(env._max_episode_steps))
print("rThresh {
}".format(env.spec.reward_threshold))
print("Número maximo de episodios {}".format(env.spec.max_episode_steps))
#1- Fire left engine
#2- Fire down engine
#3- Fire right engine
Action space is Discrete(4) Observation space is Box(-inf, inf, (8,), float32) Reward range is (-inf, inf) Obs inicial: [-0.00469522 1.4010352 -0.4755985 -0.43933803 0.00544746 0.10773007 0. 0. ] Máximo de pasos establecidos por cada episodio es 1000 rThresh 200 Número maximo de episodios 1000
| Environment Id | Observation Space | Action Space | Reward Range | tStepL | Trials | rThresh |
|---|---|---|---|---|---|---|
| LunarLander-v2 | Box(8,) | Discrete(4) | (-inf, inf) | 1000 | 100 | 200 |
Mostrar la representación vectorial de cada observación del entorno junto con la acción aleatoria seleccionada (ej. 'Observation: [..] , Action: Fire down engine'), en un intervalo de 10 episodios de 100 pasos cada uno. Opcional: visualizar los 10 episodios
env.render(), sólo posible en local from gym.wrappers import Monitor
from IPython.display import HTML
import glob
from IPython import display as ipythondisplay
def show_video(iteration):
mp4list = glob.glob('video/'+str(iteration)+'/*.mp4')
if len(mp4list) > 0:
mp4 = mp4list[0]
video = io.open(mp4, 'r+b').read()
encoded = base64.b64encode(video)
ipythondisplay.display(HTML(data='''<video alt="test" autoplay
loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>'''.format(encoded.decode('ascii'))))
else:
print("Could not find video")
def wrap_env(env, iteration):
env = Monitor(env, './video/'+str(iteration)+'/', force=True)
return env
import base64
num_episodes = 10 # number of episodes
max_steps_ep = 10000 # default max number of steps per episode (unless env has a lower hardcoded limit)
scores = []
q_estado= {
0 : 'No hacer nada',
1 : 'Encender motor izquierdo',
2 : 'Encender motor principal',
3 : 'Encender motor derecho',
}
actions = range(env.action_space.n)
for i in range(1, num_episodes+1):
env = gym.make('LunarLander-v2')
env = wrap_env(env,i)
state = env.reset()
score = 0
max_steps_ep = 0
while max_steps_ep<100:
max_steps_ep= max_steps_ep +1
action = np.random.choice(actions)
print(state)
print('Observation:'+ str(state) +',[..] , Action: '+ q_estado[action])
state, reward, done, info = env.step(action)
score += reward
if done:
break
if not done:
env.stats_recorder.save_complete()
env.stats_recorder.done = True
env.close()
print('Episode {}, score: {}'.format(i, score))
scores.append(score)
show_video(i)
[-0.00505362 1.4081988 -0.51190066 -0.12095536 0.00586276 0.11595318 0. 0. ] Observation:[-0.00505362 1.4081988 -0.51190066 -0.12095536 0.00586276 0.11595318 0. 0. ],[..] , Action: Encender motor principal [-0.01010981 1.406129 -0.511427 -0.09202451 0.01160524 0.11486121 0. 0. ] Observation:[-0.01010981 1.406129 -0.511427 -0.09202451 0.01160524 0.11486121 0. 0. ],[..] , Action: Encender motor principal [-0.01501703 1.4049863 -0.49730262 -0.0508507 0.01811743 0.13025592 0. 0. ] Observation:[-0.01501703 1.4049863 -0.49730262 -0.0508507 0.01811743 0.13025592 0. 0. ],[..] , Action: Encender motor derecho [-0.01984406 1.4032533 -0.48723984 -0.07708253 0.02260368 0.08973332 0. 0. ] Observation:[-0.01984406 1.4032533 -0.48723984 -0.07708253 0.02260368 0.08973332 0. 0. ],[..] , Action: Encender motor derecho [-0.02460146 1.400935 -0.47850528 -0.10307984 0.02533128 0.05455685 0. 0. ] Observation:[-0.02460146 1.400935 -0.47850528 -0.10307984 0.02533128 0.05455685 0. 0. ],[..] , Action: Encender motor derecho [-0.02926893 1.398013 -0.46721107 -0.12987505 0.02579436 0.00926276 0. 0. ] [...] Omitimos observaciones. [...] Observation:[-0.43387985 -0.07387536 -0.5512465 -1.311351 -0.21424979 0.1502227 1. 1. ],[..] , Action: Encender motor izquierdo [-0.43909368 -0.10260568 -0.5349258 -1.2755606 -0.20388208 0.20340443 1. 1. ] Observation:[-0.43909368 -0.10260568 -0.5349258 -1.2755606 -0.20388208 0.20340443 1. 1. ],[..] , Action: Encender motor principal Episode 1, score: -98.28223206017314
Además, he dejado en la carpeta video los diferentes videos sobre la ejecución del programa.
Ejecutar 1000 episodios con el máximo de pasos establecido en el entorno de Lunar Lander, tomando acciones de forma aleatoria. Almacenar la suma de recompensas de cada episodio y los pasos que han sido necesarios para completar el episodio. Mostrar:
- Histograma con la suma de recompensas de cada episodio
- Histograma con los pasos que han sido necesarios para completar el episodio
import base64
!pip install tqdm
num_episodes = 1000 # number of episodes
max_steps_ep = 10000 # default max number of steps per episode (unless env has a lower hardcoded limit)
scores = []
numero_pasos = []
actions = range(env.action_space.n)
from tqdm import tqdm
for i in tqdm(range(1, num_episodes+1)):
env = gym.make('LunarLander-v2')
state = env.reset()
score = 0
max_steps_ep = 0
while max_steps_ep< env._max_episode_steps:
max_steps_ep= max_steps_ep +1
action = np.random.choice(actions)
state, reward, done, info = env.step(action)
score += reward
if done:
break
env.close()
#print('Episode {}, score: {}'.format(i, score))
scores.append(score)
numero_pasos.append(max_steps_ep)
Requirement already satisfied: tqdm in /Users/rubenperezibanez/.virtualenvs/openia/lib/python3.8/site-packages
You are using pip version 9.0.1, however version 20.3.1 is available.
You should consider upgrading via the 'pip install --upgrade pip' command.
100%|██████████| 1000/1000 [00:28<00:00, 34.79it/s]
import matplotlib.pyplot as plt
plt.xlabel('Recompensa')
plt.ylabel('Cantidad')
plt.title('Histograma con la suma de recompensas de cada episodio')
plt.grid(True)
plt.hist(scores, bins =100)
plt.show()
plt.xlabel('Número de pasos')
plt.ylabel('Cantidad')
plt.title('Histograma con los pasos que han sido necesarios para completar el episodio')
plt.grid(True)
plt.hist(numero_pasos, bins= 300)
plt.axis([0, 175, 0, 100])
plt.show()
Análisis : ¿Cuál es la media de recompensas obtenida? ¿Y la media de pasos por episodio? Comenta los resultados obtenidos.
import statistics
#falta comentar
print('La media de recompensas obtenida: ' + str(statistics.mean(scores)))
print('La media de pasos por episodio: ' + str(statistics.mean(numero_pasos)))
La media de recompensas obtenida: -186.11824981551857 La media de pasos por episodio: 95.198
Análisis
De forma aleatoria hemos obtenido de media una puntuación muy baja con un número de episodios relativamente pequeño. El objetivo era conseguir un resultado mayor de 200 y hemos obtenido -186 de media
El agente aleatorio no consigue estabilizar el cohete y, por lo tanto, rápidamente desciende obteniendo una puntuación muy baja en pocos episodios.
2. Agente DDQN
En este apartado implementaremos una doble DQN. Primeramente definiremos el modelo de red neuronal, luego describiremos el comportamiento del agente, lo entrenaremos y, finalmente, testearemos el funcionamiento del agente entrenado.
2.1 Definición de la arquitectura de la red neuronal
Utilizaremos un modelo Secuencial con la siguiente configuración:
- Una primera capa completamente conectada (representada en pytorch por
nn.Lineal) de 256 neuronas ybias=True, con activación ReLU - Una segunda capa completamente conectada de 128 neuronas y
bias=True, con activación ReLU - Una tercera capa completamente conectada de 64 neuronas y
bias=True, con activación ReLU - Una última capa completamente conectada y
bias=True. Esta será nuestra capa de salida y por lo tanto tendrá tantas neuronas como dimensiones tenga nuestro espacio de acciones (una salida por cada acción posible).
Usaremos el optimizador Adam para entrenar la red.
Implementar la clase
DDQN(). Inicializar las variables necesarias y definir el modelo Secuencial de red neuronal indicado. ----------------------------------------------------------------------------------------------------------- Nota: se os proporciona el código pre-implementado. La implementación que se pide en el enunciado está indicada en los bloques TODO y/o con variables igualadas a None. class DDQN(torch.nn.Module):
###################################
###TODO: inicialización y modelo###
def __init__(self, n_inputs, n_outputs, learning_rate, actions , device='cpu'):
"""
Params
======
n_inputs: tamaño del espacio de estadps
n_outputs: tamaño del espacio de acciones
actions: array de acciones posibles
"""
super(DDQN, self).__init__()
self.device = device
self.n_inputs = None
self.n_outputs = None
self.actions = actions
self.learning_rate = learning_rate
#######################################
##TODO: Construcción de la red neuronal
self.n_inputs = n_inputs
self.n_outputs = n_outputs
self.model = None
self.model = torch.nn.Sequential(
torch.nn.Linear(self.n_inputs, 256, bias=True),
torch.nn.ReLU(),
torch.nn.Linear(256, 128, bias=True),
torch.nn.ReLU(),
torch.nn.Linear(128, 64, bias=True),
torch.nn.ReLU(),
torch.nn.Linear(64, self.n_outputs, bias=True))
#######################################
##TODO: Inicializar el optimizador
self.optimizer = None
self.optimizer = torch.optim.Adam(self.parameters(), lr=self.learning_rate)
if self.device == 'cuda':
self.model.cuda()
### Método e-greedy
def get_action(self, state, epsilon=0.05):
if np.random.random() < epsilon:
action = np.random.choice(self.actions)
else:
qvals = self.get_qvals(state)
action= torch.max(qvals, dim=-1)[1].item()
return action
def get_qvals(self, state):
if type(state) is tuple:
state = np.array([np.ravel(s) for s in state])
state_t = torch.FloatTensor(state).to(device=self.device)
return self.model(state_t)
def save(self, path, step, optimizer):
torch.save({
'step': step,
'state_dict': self.state_dict(),
'optimizer': optimizer.state_dict()
}, path)
def load(self, checkpoint_path, optimizer=None):
checkpoint = torch.load(checkpoint_path)
step = checkpoint['step']
self.load_state_dict(checkpoint['state_dict'])
if optimizer is not None:
optimizer.load_state_dict(checkpoint['optimizer'])
Definimos la clase para el buffer de repetición de experiencias del mismo modo que hacemos con la DQN clásica:
from collections import namedtuple, deque
class experienceReplayBuffer:
def __init__(self, memory_size=50000, burn_in=10000):
self.memory_size = memory_size
self.burn_in = burn_in
self.buffer = namedtuple('Buffer',
field_names=['state', 'action', 'reward', 'done', 'next_state'])
self.replay_memory = deque(maxlen=memory_size)
def sample_batch(self, batch_size=32):
samples = np.random.choice(len(self.replay_memory), batch_size,
replace=False)
# Use asterisk operator to unpack deque
batch = zip(*[self.replay_memory[i] for i in samples])
return batch
def append(self, state, action, reward, done, next_state):
self.replay_memory.append(
self.buffer(state, action, reward, done, next_state))
def burn_in_capacity(self):
return len(self.replay_memory) / self.burn_in
2.2 Definición del agente
A diferencia de la DQN clásica, en la DDQN serà la red principal la que elija la acción con mayor valor de Q, y la red objetivo la que proporcionará el valor objetivo de Q para esa acción, la que dirá qué recompensa tiene esa acción elegida por la red principal.
A continuación implementaremos una clase que defina el entrenamiento del agente teniendo en cuenta:
- La exploración/explotación (decaimiento de epsilon)
- La actualización y sincronización de la red principal y la red objetivo (pérdida)
Implementar los siguientes puntos de la clase
DDQNAgent(): - Declarar las variables de la clase
- Inicializar las variables necesarias
- Implementar la acción a tomar
- Actualizar la red principal según la frecuencia establecida en los hiperparámetros
- Calcular la pérdida teniendo en cuenta que la red principal elije la acción con mayor valor de Q, y la red objetivo proporciona el valor objetivo de Q para esa acción
- Sincronizar la red objetivo según la frecuencia establecida en los hiperparámetros
- Calcular la media de recompensas de los últimos 100 episodios
- Actualizar epsilon según: $$\textrm{max}(\epsilon · \epsilon_{\textrm{decay}}, 0.01)$$
- Las recompensas obtenidas en cada paso del entrenamiento
- Las recompensas medias de los 100 episodios anteriores
- La pérdida durante el entrenamiento
- La evolución de epsilon a lo largo del entrenamiento
from copy import deepcopy, copy
class DDQNAgent:
###################################################
######TODO 1: declarar variables ##################
def __init__(self, env, dnnetwork, buffer, epsilon=0.1, eps_decay=0.99, batch_size=32):
""""
Params
======
env: entorno
dnnetwork: clase con la red neuronal diseñada
target_network: red objetivo
buffer: clase con el buffer de repetición de experiencias
epsilon: epsilon
eps_decay: epsilon decay
batch_size: batch size
nblock: bloque de los X últimos episodios de los que se calculará la media de recompensa
reward_threshold: umbral de recompensa definido en el entorno
"""
self.env = env
self.dnnetwork = dnnetwork
#self.target_network = None
self.target_network = deepcopy(dnnetwork)
self.buffer = buffer
self.epsilon = epsilon
self.eps_decay = eps_decay
self.batch_size = batch_size
#self.nblock = none
self.nblock = 100 # bloque de los X últimos episodios de los que se calculará la media de recompensa
self.reward_threshold = self.env.spec.reward_threshold
self.initialize()
###############################################################
#####TODO 2: inicializar variables extra que se necesiten######
def initialize(self):
self.sync_eps = []
self.total_reward = 0
self.step_count = 0
self.state0 = self.env.reset()
#respuesta
self.update_loss = []
self.training_rewards = []
self.mean_training_rewards = []
#mio para epsiolons y loss
self.epsilon_conteo = []
self.loss_conteo = []
#################################################################################
######TODO 3: Tomar nueva acción ###############################################
def take_step(self, eps, mode='train'):
if mode == 'explore':
#action = None # acción aleatoria en el burn-in
action = self.env.action_space.sample()
else:
#action = None # acción a partir del valor de Q (elección de la acción con mejor Q)
action = self.dnnetwork.get_action(self.state0, eps)
self.step_count += 1
# Realización de la acción y obtención del nuevo estado y la recompensa
#new_state, reward, done, _ = None #
new_state, reward, done, _ = self.env.step(action)
self.total_reward += reward
self.buffer.append(self.state0, action, reward, done, new_state) # guardar experiencia en el buffer
self.state0 = new_state.copy()
if done:
self.state0 = env.reset()
return done
########
## Entrenamiento
def train(self, gamma=0.99, max_episodes=50000,
batch_size=32,
dnn_update_frequency=4,
dnn_sync_frequency=2000):
self.gamma = gamma
# Rellenamos el buffer con N experiencias aleatorias ()
print("Filling replay buffer...")
while self.buffer.burn_in_capacity() < 1:
self.take_step(self.epsilon, mode='explore')
episode = 0
training = True
print("Training...")
while training:
self.state0 = self.env.reset()
self.total_reward = 0
gamedone = False
while gamedone == False:
# El agente toma una acción
gamedone = self.take_step(self.epsilon, mode='train')
#################################################################################
#####TODO 4: Actualizar la red principal según la frecuencia establecida #######
# Actualizamos la red principal según la frecuencia establecida
if self.step_count % dnn_update_frequency == 0:
self.update()
########################################################################################
###TODO 6: Sincronizar red principal y red objetivo según la frecuencia establecida#####
# Sincronizamos red principal y red objetivo según la frecuencia establecida
if self.step_count % dnn_sync_frequency == 0:
self.target_network.load_state_dict(
self.dnnetwork.state_dict())
self.sync_eps.append(episode)
if gamedone:
episode += 1
##################################################################
########TODO: Almacenar epsilon, training rewards y pérdida#######
self.training_rewards.append(self.total_reward) # guardamos las recompensas obtenidas
self.epsilon_conteo.append(self.epsilon) #NUEVO
self.loss_conteo.append(self.update_loss[-1]) #NUEVO
#######################################################################################
###TODO 7: calcular la media de recompensa de los últimos X episodios, y almacenar#####
mean_rewards = None
mean_rewards = np.mean( # calculamos la media de recompensa de los últimos X episodios
self.training_rewards[-self.nblock:])
self.mean_training_rewards.append(mean_rewards)
print("\rEpisode {:d} Mean Rewards {:.2f} Epsilon {}\t\t".format(
episode, mean_rewards, self.epsilon), end="")
# Comprobamos que todavía quedan episodios
self.update_loss = []
print("\rEpisode {:d} Mean Rewards {:.2f} Epsilon {}\t\t".format(
episode, mean_rewards, self.epsilon), end="")
# Comprobamos que todavía quedan episodios
if episode >= max_episodes:
training = False
print('\nEpisode limit reached.')
break
# Termina el juego si la media de recompensas ha llegado al umbral fijado para este juego
if mean_rewards >= self.reward_threshold:
training = False
print('\nEnvironment solved in {} episodes!'.format(
episode))
break
#################################################################################
######TODO 8: Actualizar epsilon según la velocidad de decaimiento fijada########
self.epsilon = max(self.epsilon * self.eps_decay, 0.01)
## Cálculo de la pérdida
def calculate_loss(self, batch):
# Separamos las variables de la experiencia y las convertimos a tensores
states, actions, rewards, dones, next_states = [i for i in batch]
rewards_vals = torch.FloatTensor(rewards).to(device=self.dnnetwork.device).reshape(-1,1)
actions_vals = torch.LongTensor(np.array(actions)).reshape(-1,1).to(
device=self.dnnetwork.device)
dones_t = torch.ByteTensor(dones).to(device=self.dnnetwork.device)
# Obtenemos los valores de Q de la red principal
qvals = torch.gather(self.dnnetwork.get_qvals(states), 1, actions_vals)
#############################################################################
#########TODO 5: DDQN update ################################################
next_actions = torch.max(self.dnnetwork.get_qvals(next_states), dim=-1)[1] #Obtenemos la acción con máximo valor de Q de la red principal
next_actions_vals = torch.LongTensor(next_actions).reshape(-1,1).to(
device=self.dnnetwork.device)
target_qvals = self.target_network.get_qvals(next_states) # Obtenemos los valores de Q de la red objetivo
qvals_next = torch.gather(target_qvals, 1, next_actions_vals).detach()
#############################################################################
qvals_next[dones_t] = 0
# Calculamos ecuación de Bellman
expected_qvals = self.gamma * qvals_next + rewards_vals
# Calculamos la pérdida
loss = torch.nn.MSELoss()(qvals, expected_qvals.reshape(-1,1))
return loss
def update(self):
self.dnnetwork.optimizer.zero_grad() # eliminamos cualquier gradiente pasado
batch = self.buffer.sample_batch(batch_size=self.batch_size) # seleccionamos un conjunto del buffer
loss = self.calculate_loss(batch) # calculamos la pérdida
loss.backward() # hacemos la diferencia para obtener los gradientes
self.dnnetwork.optimizer.step() # aplicamos los gradientes a la red neuronal
# Guardamos los valores de pérdida
if self.dnnetwork.device == 'cuda':
self.update_loss.append(loss.detach().cpu().numpy())
else:
self.update_loss.append(loss.detach().numpy())
def plot_rewards(self):
plt.figure(figsize=(12,8))
plt.plot(self.training_rewards, label='Rewards')
plt.plot(self.mean_training_rewards, label='Mean Rewards')
plt.axhline(self.reward_threshold, color='r', label="Reward threshold")
plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.legend(loc="upper left")
plt.show()
def plot_loss(self):
plt.figure(figsize=(12,8))
plt.plot(self.loss_conteo, label='Perdidas')
plt.xlabel('Episodes')
plt.ylabel('loss')
plt.legend(loc="upper left")
plt.show()
def plot_epsilon(self):
plt.figure(figsize=(12,8))
plt.plot(self.epsilon_conteo, label='epsilon')
plt.xlabel('Episodes')
plt.ylabel('Epsilpn')
plt.legend(loc="upper left")
plt.show()
#store
def save(self, step, logs_path):
os.makedirs(logs_path, exist_ok=True)
model_list = glob.glob(os.path.join(logs_path, '*.pth'))
logs_path = os.path.join(logs_path, 'model-{
}.pth' .format(step))
self.dnnetwork.save(logs_path, step=step, optimizer=self.dnnetwork.optimizer)
print('=> Save {
}' .format(logs_path))
def restore(self, logs_path):
self.dnnetwork.load(logs_path)
self.target_network.load(logs_path)
print('=> Restore {}' .format(logs_path))
2.3 Entrenamiento
A continuación entrenaremos el modelo con los siguientes hiperparámetros:
- Velocidad de aprendizaje: 25*10^-5
- Tamaño del batch: 32
- Capacidad máxima del buffer: 10000
- Gamma: 0.99
- Epsilon: 1, con decaimiento de 0.99
- Número máximo de episodios: 3000
- Número de episodios para rellenar el buffer: 1000
- Frecuencia de actualización de la red neuronal: 5
- Frecuencia de sincronización con la red objetivo: 1000
Declarar los hiperparámetros, cargar el modelo de red neuronal y entrenar el agente
lr = 25*10**(-5) #Velocidad aprendizaje
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
MAX_EPISODES = 3000 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 32 #Conjunto a coger del buffer para la red neuronal
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000 #Frecuencia de sincronización de pesos entre red neuronal y red objetivo
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('Cargamos el modelo de red neuronal:')
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN(n_inputs,n_outputs, lr, np.arange(env.action_space.n))
print('Creamos nuestro agente:')
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
print('Entrenamos el agente con los hiperparámetros establecidos:')
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
agent_DDQN = deepcopy(agent)
Cargamos el modelo de red neuronal: Creamos nuestro agente: Entrenamos el agente con los hiperparámetros establecidos: Filling replay buffer... Training... Episode 2 Mean Rewards -159.57 Epsilon 0.99
<ipython-input-87-96f1642efca0>:187: UserWarning: indexing with dtype torch.uint8 is now deprecated, please use a dtype torch.bool instead. (Triggered internally at ../aten/src/ATen/native/IndexingUtils.h:25.) qvals_next[dones_t] = 0
Episode 706 Mean Rewards 202.11 Epsilon 0.01 118606165716 Environment solved in 706 episodes!
Representar:
- Gráfico con las recompensas obtenidas a lo largo del entrenamieno, la evolución de las recompensas medias cada 100 episodios, y el umbral de recompensa establecido por el entorno.
- Gráfico con la evolución de la perdida a lo largo del entrenamiento
- Gráfico con la evolución de epsilon a lo largo del entrenamiento
agent.plot_rewards()
agent.plot_loss()
agent.plot_epsilon()
Análisis: Guardar el modelo entrenado en formato ".pth" y comentar los resultados obtenidos.
import os
agent.save('','test')
agent.restore('test/model-.pth')
=> Save test/model-.pth => Restore test/model-.pth
El entrenamiento del agente ha sido muy rápido y la media de las recompensas ha subido muy rápidamente del episodio 0 al 300. A partir de ese momento, cuando ha alcanzado un Epsilon cercano al 0.01 al sistema le costaba más aumentar la media de las recompensas.
Respecto a las pérdidas, un aumento alrededor el episodio 500 ha aumentado el tiempo del entrenamiento.
2.4 Test del agente entrenado
Una vez entrenado el agente, nos interesa comprobar cómo de bien ha aprendido, si el "robot" es capaz de realizar las tareas aprendidas. Para ello, recuperamos el modelo entrenado y dejamos que el agente tome acciones aleatorias según ese modelo y observamos su comportamiento.
Cargar el modelo entrenado y ejecutar el agente entrenado durante 100 episodios consecutivos. Calcular la suma de recompensas por cada episodio. Mostrar en un gráfico la suma de las recompensas respecto de los episodios, incluyendo el umbral de recompensa establecido por el entorno. --------------------------------------------------------------------------------------------------- Opcional: visualizar los episodios con
env.render(), sólo posible en local. Esta visualización ralentiza el proceso unos segundos por episodio. En la carpeta videoDDQNAgent se pueden encontrar todas las visualizaciones del agente
import base64
def show_video(iteration):
mp4list = glob.glob('videoDDQNAgent/'+str(iteration)+'/*.mp4')
if len(mp4list) > 0:
mp4 = mp4list[0]
video = io.open(mp4, 'r+b').read()
encoded = base64.b64encode(video)
ipythondisplay.display(HTML(data='''<video alt="test" autoplay
loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>'''.format(encoded.decode('ascii'))))
else:
print("Could not find video")
def wrap_env(env, iteration):
env = Monitor(env, './videoDDQNAgent/'+str(iteration)+'/', force=True)
return env
num_episodes = 100 # number of episodes
max_steps_ep = 10000 # default max number of steps per episode (unless env has a lower hardcoded limit)
numero_pasos = []
umbral_recompensa = []
scores = []
actions = range(env.action_space.n)
for i in tqdm(range(1, num_episodes+1)):
env = gym.make('LunarLander-v2')
max_episodios_entorno = env._max_episode_steps
umbral_recompensa.append(env.spec.reward_threshold)
env = wrap_env(env,i)
state = env.reset()
score = 0
max_steps_ep = 0
while max_steps_ep< max_episodios_entorno:
max_steps_ep= max_steps_ep +1
action = agent.dnnetwork.get_action(state,agent.epsilon)
state, reward, done, info = env.step(action)
score += reward
if done:
break
if not done:
env.stats_recorder.save_complete()
env.stats_recorder.done = True
env.close()
scores.append(score)
numero_pasos.append(max_steps_ep)
print('Video Final de ejemplo')
show_video(i)
100%|██████████| 100/100 [23:09<00:00, 13.89s/it]
Video Final de ejemplo
plt.figure(figsize=(12,8))
plt.plot(scores, label='Rewards')
plt.axhline(200, color='r', label="Reward threshold")
plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.legend(loc="upper left")
plt.show()
plt.xlabel('Recompensa')
plt.ylabel('Cantidad')
plt.title('Histograma con la suma de recompensas de cada episodio')
plt.grid(True)
plt.axvline(200, color='k', linestyle='dashed', linewidth=3)
plt.hist(scores, bins =40)
plt.axis([0, 350, 0, 20])
plt.show()
Análisis: Comenta el comportamiento del agente entrenado a lo largo de estos 100 episodios
El comportamiento obtenido por el agente ha sido correcto en la mayoría de las ocasiones. Como se puede observar en la gráfica, solamente en 8 ocasiones obtenemos una recompensa por debajo de 200 y, por lo tanto, he considerado al agente como útil para resolver el juego (92 % tasa de acierto).
El entrenamiento del agente ha sido muy rápido y la media de las recompensas ha subido muy rápidamente del episodio 0 al 300. A partir de ese momento, cuando ha alcanzado un Epsilon cercano al 0.01 al sistema le costaba más aumentar la media de las recompensas.
3. Agente Dueling DQN
En este apartado resolveremos el mismo entorno con las mismas características para el agente, pero usando una dueling DQN. Como en el caso anterior, primero definiremos el modelo de red neuronal, luego describiremos el comportamiento del agente, lo entrenaremos y, finalmente, testearemos el funcionamiento del agente entrenado.
3.1 Definición de la arquitectura de la red neuronal
El objetivo principal de las dueling DQN es "ahorrarse" el cálculo del valor de Q en aquéllos estados en los que es irrelevante la acción que se tome. Para ello se descompone la función Q en dos componentes:
$$Q(s, a) = A(s, a) + V (s)$$Esta descomposición se realiza a nivel de la arquitectura de la red neuronal. Las primeras capas que teníamos en la DDQN serán comunes, y luego la red se dividirá en dos partes separadas definidas por el resto de capas. Para ello, en lugar de usar un modelo Secuencial, usaremos un modelo Funcional el cual nos permite agregar resultados de redes separadas. En un modelo Funcional en pytorch se define primero el esqueleto de la arquitectura, las capas, y luego se define cómo fluirán los datos a través de esta arquitectura, es decir, cómo se conectan estas capas entre ellas, i.e. las funciones de activación. Ésto último queda descrito en una función forward().
Por ejemplo, el siguiente modelo Sequential de dos capas completamente conectadas (fully connected) y activación ReLU:
model = nn.Sequential(nn.Linear(8, 16),
nn.ReLU(),
nn.Linear(16, 2))
es equivalente en Functional a:
def __init__(self):
self.fc = torch.nn.Linear(8, 16)
self.fc2 = torch.nn.Linear(16,2)
def forward(self, state):
x = torch.nn.functional.relu(self.fc1(state))
x=self.fc2(x)
return x
La descomposición en sub-redes del modelo de la DDQN implementada en el apartado anterior, será entonces:
- Bloque común:
- Una primera capa completamente conectada de 256 neuronas y
bias=True, con activación ReLU - Una segunda capa completamente conectada de 128 neuronas y
bias=True, con activación ReLU - Por cada una de las subredes de ventaja A(s,a) y valor V(s):
- Una capa completamente conectada de 64 neuronas y
bias=True, con activación ReLU - Una última capa completamente conectada y
bias=True. Esta será nuestra capa de salida y por lo tanto el número de neuronas de salida dependerá de si se trata de la red A(s,a) que tendrá tantas neuronas como dimensiones tenga el espacio de acciones, o si se trata de la red V(s), con un valor por estado.
Importamos el paquete functional de torch:
import torch.nn.functional as F
Ejercicio : Implementar la clase
duelingDQN(). Inicializar las variables necesarias y definir el modelo Funcional de red neuronal indicado. ----------------------------------------------------------------------------------------------------------- Nota: se os proporciona el código pre-implementado. La implementación que se pide en el enunciado está indicada en los bloques TODO y/o con variables igualadas a None. class duelingDQN(torch.nn.Module):
###################################
####TODO: Inicializar variables####
def __init__(self, env,lr ,device='cpu'):
"""
Params
======
n_inputs: tamaño del espacio de estadps
n_outputs: tamaño del espacio de acciones
actions: array de acciones posibles
"""
super(duelingDQN, self).__init__()
self.device = device
#self.n_inputs = None
self.n_inputs = env.observation_space.shape[0]
#self.n_outputs = None
self.n_outputs = env.action_space.n
self.actions = np.arange(env.action_space.n)
#self.actions = None
#####
##########################################
##TODO: Construcción de la red neuronal###
#Red común
'''
self.fc = torch.nn.Sequential(
torch.nn.Linear(self.n_inputs, 256, bias=True)
torch.nn.ReLU()
)
self.fc2 = torch.nn.Sequential(
torch.nn.Linear(256, 128, bias=True)
torch.nn.ReLU()
)
'''
self.fc = torch.nn.Linear(self.n_inputs, 256, bias=True)
self.fc2 = torch.nn.Linear(256, 128, bias=True)
# Sub-red de la función de Valor
self.fc_v1 = torch.nn.Linear(128, 64, bias=True)
self.fc_v = torch.nn.Linear(64, self.n_outputs, bias=True)
'''
self.fc_v = torch.nn.Sequential(
torch.nn.Linear(128, 64, bias=True),
torch.nn.ReLU(),
torch.nn.Linear(64, self.n_outputs, bias=True)
)
'''
# Sub-red de la Ventaja A(s,a)
self.fc_advantage1= torch.nn.Linear(128, 64, bias=True)
self.fc_advantage= torch.nn.Linear(64, 1, bias=True)
'''
self.fc_advantage = torch.nn.Sequential(
torch.nn.Linear(128, 64, bias=True),
torch.nn.ReLU(),
torch.nn.Linear(64, 1, bias=True)
)
'''
self.optimizer = torch.optim.Adam(self.parameters(), lr=lr)
#######################################
#####TODO: función forward#############
def forward(self, state):
'''
out = self.head(x)
val_out = self.val(out).reshape(out.shape[0], 1)
adv_out = self.adv(out).reshape(out.shape[0], -1)
adv_mean = adv_out.mean(dim=1, keepdim=True)
q = val_out + adv_out - adv_mean
'''
#return q
#Conexión entre capas Red común
x = torch.nn.functional.relu(self.fc(state))
x = self.fc2(x)
x = torch.nn.functional.relu(x)
#Conexión entre capas Sub-red Valor
val_out1 = torch.nn.functional.relu(self.fc_v1(x))#.reshape(out.shape[0], 1)
val_out = self.fc_v(val_out1)
'''
val_out = self.fc_v(x)
'''
#Conexión entre capas Sub-red Ventaja
'''
adv = self.fc_advantage(x)#.reshape(out.shape[0], -1)
'''
adv = torch.nn.functional.relu(self.fc_advantage1(x))
adv = self.fc_advantage(adv)
#Agregar las dos subredes: Q(s,a) = V(s) + (A(s,a) - 1/|A| * sum A(s,a'))
#action = None
action = val_out + (adv - adv.mean())
return action
#########
if self.device == 'cuda':
self.model.cuda()
### Método e-greedy
def get_action(self, state, epsilon=0.05):
if np.random.random() < epsilon:
action = np.random.choice(self.actions)
else:
qvals = self.get_qvals(state)
action= torch.max(qvals, dim=-1)[1].item()
return action
def get_qvals(self, state):
if type(state) is tuple:
state = np.array([np.ravel(s) for s in state])
state_t = torch.FloatTensor(state).to(device=self.device)
return self.forward(state_t)
#por mi
def save(self, path, step, optimizer):
torch.save({
'step': step,
'state_dict': self.state_dict(),
'optimizer': optimizer.state_dict()
}, path)
def load(self, checkpoint_path, optimizer=None):
checkpoint = torch.load(checkpoint_path)
step = checkpoint['step']
self.load_state_dict(checkpoint['state_dict'])
if optimizer is not None:
optimizer.load_state_dict(checkpoint['optimizer'])
Para el buffer de repetición de experiencias podemos usar exactamente la misma clase experienceReplayBuffer descrita en el apartado anterior de la DDQN.
3.2 Definición del agente
La diferencia entre la DDQN y la dueling DQN se centra, como hemos visto, en la definición de la arquitectura de la red. Pero el proceso de aprendizaje y actualización es exactamente el mismo. Así, podemos recuperar la clase implementada en el apartado anterior, DDQNAgent() y reutilizarla aquí bajo el nombre de duelingDQNAgent(). Lo único que deberemos hacer es añadir el optimizador entre las variables a declarar y adaptar la función de pérdida al formato Functional de pytorch.
Ejercicio (1 pto): Implementar la clase
duelingDQNAgent() como la DDQNAgent(), teniendo en cuenta los siguientes cambios: - Inicializar variables necesarias
- Inicializar el optimizador Adam junto con las otras variables de la clase
- Cambiar la función de loss del modo Sequential
loss = torch.nn.MSELoss()(qvals, expected_qvals.reshape(-1,1))a formato Functional:loss = F.mse_loss(qvals, expected_qvals.reshape(-1,1))
- Las recompensas obtenidas en cada paso del entrenamiento
- Las recompensas medias de los 100 episodios anteriores
- La pérdida durante el entrenamiento
- La evolución de epsilon a lo largo del entrenamiento
##TODO:
from copy import deepcopy, copy
class duelingDQNAgent:
"""
Params
======
env: entorno
dnnetwork: clase con la red neuronal diseñada
target_network: red objetivo
buffer: clase con el buffer de repetición de experiencias
lr: learing rate
epsilon: epsilon
eps_decay: epsilon decay
batch_size: batch size
nblock: bloque de los X últimos episodios de los que se calculará la media de recompensa
reward_threshold: umbral de recompensa definido en el entorno
"""
def __init__(self, env, dnnetwork, buffer, epsilon=0.1, eps_decay=0.99, batch_size=32, lr= 25*10**(-5)): #Velocidad aprendizaje):
self.env = env
self.dnnetwork = dnnetwork
#self.target_network = None
self.target_network = deepcopy(dnnetwork)
self.buffer = buffer
self.epsilon = epsilon
self.eps_decay = eps_decay
self.batch_size = batch_size
self.lr= lr
#self.nblock = none
self.nblock = 100 # bloque de los X últimos episodios de los que se calculará la media de recompensa
self.reward_threshold = self.env.spec.reward_threshold
self.initialize()
###############################################################
#####TODO 2: inicializar variables extra que se necesiten######
def initialize(self):
self.sync_eps = []
self.total_reward = 0
self.step_count = 0
self.state0 = self.env.reset()
#respuesta
self.update_loss = []
self.training_rewards = []
self.mean_training_rewards = []
#mio para epsiolons y loss
self.epsilon_conteo = []
self.loss_conteo = []
#################################################################################
######TODO 3: Tomar nueva acción ###############################################
def take_step(self, eps, mode='train'):
if mode == 'explore':
#action = None # acción aleatoria en el burn-in
action = self.env.action_space.sample()
else:
#action = None # acción a partir del valor de Q (elección de la acción con mejor Q)
action = self.dnnetwork.get_action(self.state0, eps)
self.step_count += 1
# Realización de la acción y obtención del nuevo estado y la recompensa
#new_state, reward, done, _ = None #
new_state, reward, done, _ = self.env.step(action)
self.total_reward += reward
self.buffer.append(self.state0, action, reward, done, new_state) # guardar experiencia en el buffer
self.state0 = new_state.copy()
if done:
self.state0 = env.reset()
return done
########
## Entrenamiento
def train(self, gamma=0.99, max_episodes=50000,
batch_size=32,
dnn_update_frequency=4,
dnn_sync_frequency=2000):
self.gamma = gamma
# Rellenamos el buffer con N experiencias aleatorias ()
print("Filling replay buffer...")
while self.buffer.burn_in_capacity() < 1:
self.take_step(self.epsilon, mode='explore')
episode = 0
training = True
print("Training...")
while training:
self.state0 = self.env.reset()
self.total_reward = 0
gamedone = False
while gamedone == False:
# El agente toma una acción
gamedone = self.take_step(self.epsilon, mode='train')
#################################################################################
#####TODO 4: Actualizar la red principal según la frecuencia establecida #######
# Actualizamos la red principal según la frecuencia establecida
if self.step_count % dnn_update_frequency == 0:
self.update()
########################################################################################
###TODO 6: Sincronizar red principal y red objetivo según la frecuencia establecida#####
# Sincronizamos red principal y red objetivo según la frecuencia establecida
if self.step_count % dnn_sync_frequency == 0:
self.target_network.load_state_dict(
self.dnnetwork.state_dict())
self.sync_eps.append(episode)
if gamedone:
episode += 1
##################################################################
########TODO: Almacenar epsilon, training rewards y pérdida#######
self.epsilon_conteo.append(self.epsilon) #NUEVO
self.loss_conteo.append(self.update_loss[-1]) #NUEVO
self.training_rewards.append(self.total_reward) # guardamos las recompensas obtenidas
#######################################################################################
###TODO 7: calcular la media de recompensa de los últimos X episodios, y almacenar#####
mean_rewards = None
mean_rewards = np.mean( # calculamos la media de recompensa de los últimos X episodios
self.training_rewards[-self.nblock:])
self.mean_training_rewards.append(mean_rewards)
print("\rEpisode {:d} Mean Rewards {:.2f} Epsilon {}\t\t".format(
episode, mean_rewards, self.epsilon), end="")
# Comprobamos que todavía quedan episodios
self.update_loss = []
print("\rEpisode {:d} Mean Rewards {:.2f} Epsilon {}\t\t".format(
episode, mean_rewards, self.epsilon), end="")
# Comprobamos que todavía quedan episodios
if episode >= max_episodes:
training = False
print('\nEpisode limit reached.')
break
# Termina el juego si la media de recompensas ha llegado al umbral fijado para este juego
if mean_rewards >= self.reward_threshold:
training = False
print('\nEnvironment solved in {} episodes!'.format(
episode))
break
#################################################################################
######TODO 8: Actualizar epsilon según la velocidad de decaimiento fijada########
self.epsilon = max(self.epsilon * self.eps_decay, 0.01)
## Cálculo de la pérdida
def calculate_loss(self, batch):
# Separamos las variables de la experiencia y las convertimos a tensores
states, actions, rewards, dones, next_states = [i for i in batch]
rewards_vals = torch.FloatTensor(rewards).to(device=self.dnnetwork.device).reshape(-1,1)
actions_vals = torch.LongTensor(np.array(actions)).reshape(-1,1).to(
device=self.dnnetwork.device)
dones_t = torch.ByteTensor(dones).to(device=self.dnnetwork.device)
# Obtenemos los valores de Q de la red principal
qvals = torch.gather(self.dnnetwork.get_qvals(states), 1, actions_vals)
#############################################################################
#########TODO 5: DDQN update ################################################
next_actions = torch.max(self.dnnetwork.get_qvals(next_states), dim=-1)[1] #Obtenemos la acción con máximo valor de Q de la red principal
next_actions_vals = torch.LongTensor(next_actions).reshape(-1,1).to(
device=self.dnnetwork.device)
target_qvals = self.target_network.get_qvals(next_states) # Obtenemos los valores de Q de la red objetivo
qvals_next = torch.gather(target_qvals, 1, next_actions_vals).detach()
#############################################################################
qvals_next[dones_t] = 0
# Calculamos ecuación de Bellman
expected_qvals = self.gamma * qvals_next + rewards_vals
# Calculamos la pérdida
loss = torch.nn.functional.mse_loss(qvals, expected_qvals.reshape(-1,1))
return loss
def update(self):
self.dnnetwork.optimizer.zero_grad() # eliminamos cualquier gradiente pasado
batch = self.buffer.sample_batch(batch_size=self.batch_size) # seleccionamos un conjunto del buffer
loss = self.calculate_loss(batch) # calculamos la pérdida
loss.backward() # hacemos la diferencia para obtener los gradientes
self.dnnetwork.optimizer.step() # aplicamos los gradientes a la red neuronal
# Guardamos los valores de pérdida
if self.dnnetwork.device == 'cuda':
self.update_loss.append(loss.detach().cpu().numpy())
else:
self.update_loss.append(loss.detach().numpy())
def plot_rewards(self):
plt.figure(figsize=(12,8))
plt.plot(self.training_rewards, label='Rewards')
plt.plot(self.mean_training_rewards, label='Mean Rewards')
plt.axhline(self.reward_threshold, color='r', label="Reward threshold")
plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.legend(loc="upper left")
plt.show()
def plot_loss(self):
plt.figure(figsize=(12,8))
plt.plot(self.loss_conteo, label='Perdidas')
plt.xlabel('Episodes')
plt.ylabel('loss')
plt.legend(loc="upper left")
plt.show()
def plot_epsilon(self):
plt.figure(figsize=(12,8))
plt.plot(self.epsilon_conteo, label='epsilon')
plt.xlabel('Episodes')
plt.ylabel('Epsilpn')
plt.legend(loc="upper left")
plt.show()
#store
def save(self, step, logs_path):
os.makedirs(logs_path, exist_ok=True)
model_list = glob.glob(os.path.join(logs_path, '*.pth'))
logs_path = os.path.join(logs_path, 'model-{}.pth' .format(step))
self.dnnetwork.save(logs_path, step=step, optimizer=self.dnnetwork.optimizer)
print('=> Save {}' .format(logs_path))
def restore(self, logs_path):
self.dnnetwork.load(logs_path)
self.target_network.load(logs_path)
print('=> Restore {}' .format(logs_path))
3.3 Entrenamiento
A continuación entrenaremos el modelo dueling DQN con los mismos hiperparámetros con los que entrenamos la DDQN.
Cargar el modelo de red neuronal y entrenar el agente con los mismos hiperparámetros usados para la DDQN
lr = 25*10**(-5) #Velocidad aprendizaje
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
MAX_EPISODES = 3000 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 32 #Conjunto a coger del buffer para la red neuronal
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000 #Frecuencia de sincronización de pesos entre red neuronal y red objetivo
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('Cargamos el modelo de red neuronal:')
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
duelingDQN = duelingDQN(env,lr)
print('Creamos nuestro agente:')
agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
print('Entrenamos el agente con los hiperparámetros establecidos:')
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
agent_duelingDQN = deepcopy(agent)
Cargamos el modelo de red neuronal: Creamos nuestro agente: Entrenamos el agente con los hiperparámetros establecidos: Filling replay buffer... Training... Episode 2 Mean Rewards -232.21 Epsilon 0.99
<ipython-input-28-bd3d70f337a8>:191: UserWarning: indexing with dtype torch.uint8 is now deprecated, please use a dtype torch.bool instead. (Triggered internally at ../aten/src/ATen/native/IndexingUtils.h:25.) qvals_next[dones_t] = 0
Episode 410 Mean Rewards 201.28 Epsilon 0.016398140018627688 Environment solved in 410 episodes!
Mostrar los mismos gráficos que con la DDQN:
- Recompensas obtenidas a lo largo del entrenamieno y la evolución de las recompensas medias cada 100 episodios, junto con el umbral de recompensa establecido por el entorno
- Pérdida durante el entrenamiento
- Evolución de epsilon a lo largo del entrenamiento
agent_duelingDQN.plot_rewards()
print('Pérdidas, hay un error en el gráfico. Simboliza las pérdidas el siguiente gráfico.')
agent_duelingDQN.plot_loss()
agent_duelingDQN.plot_epsilon()
Pérdidas, hay un error en el gráfico. Simboliza las pérdidas el siguiente gráfico.
Análisis: Guardar el modelo entrenado en formato ".pth" y comentar los resultados obtenidos.
import os
agent.save('','Modelo-duelingDQN')
agent.restore('Modelo-duelingDQN/model-.pth')
=> Save Modelo-duelingDQN/model-.pth => Restore Modelo-duelingDQN/model-.pth
Análisis
Cómo se informa en la teoría, el entrenamiento de este modelo ha sido más rápido que el llevado a cabo por el modelo DDQN. Realmente hemos conseguido obtener un modelo excelente en una cantidad de episodios más reducidas debido a la descomposición de la función Q.
Exactamente hemos pasado de 700 episodios obtenidos en el modelo DDQN a 410 obtenidos en el Dueling DQN.
Además, la curva Epsilon ha sido más lineal que en el modelo anterior. Esto es debido a que se obtiene un modelo entrenado más rápidamente.
Por último, en las perdidas he detectado un leve aumento al final que ha generado que el modelo tarde un poco más el entrenamiento.
3.4 Test del agente
Finalmente analizamos el comportamiento del agente entrenado.
Cargar el modelo entrenado y ejecutar el agente entrenado durante 100 episodios consecutivos. Calcular la suma de recompensas por cada episodio. Mostrar en un gráfico la suma de las recompensas respecto de los episodios, incluyendo el umbral de recompensa establecido por el entorno. --------------------------------------------------------------------------------------------------- Opcional: visualizar los episodios con
env.render(), sólo posible en local. Esta visualización ralentiza el proceso unos segundos por episodio. import base64
def show_video(iteration):
mp4list = glob.glob('videoduelingDQN/'+str(iteration)+'/*.mp4')
if len(mp4list) > 0:
mp4 = mp4list[0]
video = io.open(mp4, 'r+b').read()
encoded = base64.b64encode(video)
ipythondisplay.display(HTML(data='''<video alt="test" autoplay
loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>'''.format(encoded.decode('ascii'))))
else:
print("Could not find video")
def wrap_env(env, iteration):
env = Monitor(env, './videoduelingDQN/'+str(iteration)+'/', force=True)
return env
import base64
from tqdm import tqdm
num_episodes = 100 # number of episodes
max_steps_ep = 10000 # default max number of steps per episode (unless env has a lower hardcoded limit)
numero_pasos = []
umbral_recompensa = []
scores = []
env = gym.make('LunarLander-v2')
actions = range(env.action_space.n)
for i in tqdm(range(1, num_episodes+1)):
env = gym.make('LunarLander-v2')
max_episodios_entorno = env._max_episode_steps
umbral_recompensa.append(env.spec.reward_threshold)
env = wrap_env(env,i)
state = env.reset()
score = 0
max_steps_ep = 0
while max_steps_ep< max_episodios_entorno:
max_steps_ep= max_steps_ep +1
action = agent.dnnetwork.get_action(state,agent.epsilon)
state, reward, done, info = env.step(action)
score += reward
if done:
break
if not done:
env.stats_recorder.save_complete()
env.stats_recorder.done = True
env.close()
#print('Episode {}, score: {}'.format(i, score))
scores.append(score)
numero_pasos.append(max_steps_ep)
print('Muestro la última imagen')
show_video(i)
100%|██████████| 100/100 [12:02<00:00, 7.22s/it]
Muestro la última imagen
plt.figure(figsize=(12,8))
plt.plot(scores, label='Rewards')
plt.axhline(200, color='r', label="Reward threshold")
plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.legend(loc="upper left")
plt.show()
plt.xlabel('Recompensa')
plt.ylabel('Cantidad')
plt.title('Histograma con la suma de recompensas de cada episodio')
plt.grid(True)
plt.axvline(200, color='k', linestyle='dashed', linewidth=3)
plt.hist(scores, bins =40)
plt.axis([0, 350, 0, 20])
plt.show()
Análisis: Comenta los resultados obtenidos.
Análisis
Cómo ya se ha informado, el entrenamiento de este modelo ha sido más rápido que el llevado a cabo por el modelo DDQN. Realmente hemos conseguido obtener un modelo excelente en una cantidad de episodios más reducidas debido a la descomposición de la función Q.
Pero no solo eso, hemos obtenido un mejor agente ya que hemos obtenido un 100% de éxitos con el agente. Los resultados han sido muy bueno, además de eficientes en el entrenamiento. Todo ello unido me hace pensar que este modelo es la mejor solución al problema.
4. REINFORCE with baseline
En este apartado implementaremos el último de los tres modelos, pero este basado en Gradientes de Política. Usaremos el método de REINFORCE con una línea de base que sea la media estandardizada del retorno.
4.1 Definición de la arquitectura de la red neuronal
Utilizaremos un modelo Secuencial con la siguiente configuración:
- Una primera capa completamente conectada de 16 neuronas y
bias=True, con activación Tanh - Una segunda capa completamente conectada de 32 neuronas y
bias=True, con activación Tanh - Una última capa completamente conectada con tantas neuronas como dimensiones tenga nuestro espacio de acciones (una salida por cada acción posible),
bias=True, y activación Softmax (dim=-1)
Usaremos el optimizador Adam para entrenar la red.
Implementar la clase
PGReinforce(). Inicializar las variables necesarias y definir el modelo Secuencial de red neuronal indicado. ----------------------------------------------------------------------------------------------------------- Nota: se os proporciona el código pre-implementado. La implementación que se pide en el enunciado está indicada en los bloques TODO y/o con variables igualadas a None. class PGReinforce(torch.nn.Module):
###################################
####TODO: Inicializar variables####
def __init__(self, env, learning_rate=1e-3, device='cpu'):
"""
Params
======
n_inputs: tamaño del espacio de estadps
n_outputs: tamaño del espacio de acciones
actions: array de acciones posibles
"""
super(PGReinforce, self).__init__()
self.device=device
#self.n_inputs = None
self.n_inputs = env.observation_space.shape[0]
#self.n_outputs = None
self.n_outputs = env.action_space.n
self.actions = np.arange(env.action_space.n)
self.learning_rate = learning_rate
#######################################
##TODO: Construcción de la red neuronal
self.model = None
self.model = torch.nn.Sequential(
torch.nn.Linear(self.n_inputs, 16, bias=True),
torch.nn.Tanh(),
torch.nn.Linear(16, 32, bias=True),
torch.nn.Tanh(),
torch.nn.Linear(32, self.n_outputs, bias=True),
torch.nn.Softmax(dim=-1)
)
#####
#######################################
##TODO: Inicializar el optimizador
#self.optimizer = None
self.optimizer = torch.optim.Adam(self.parameters(), lr=lr)
####
if self.device == 'cuda':
self.model.cuda()
#Obtención de las probabilidades de las posibles acciones
def get_action_prob(self, state):
action_probs = self.model(torch.FloatTensor(state))
return action_probs
def save(self, path, step, optimizer):
torch.save({
'step': step,
'state_dict': self.state_dict(),
'optimizer': optimizer.state_dict()
}, path)
def load(self, checkpoint_path, optimizer=None):
checkpoint = torch.load(checkpoint_path)
step = checkpoint['step']
self.load_state_dict(checkpoint['state_dict'])
if optimizer is not None:
optimizer.load_state_dict(checkpoint['optimizer'])
4.2 Definición del agente
Ejercicio (1 pto): Implementar los siguientes puntos de la clase
reinforceAgent(): - Declarar las variables de la clase
- Inicializar las variables necesarias
- Implementar la acción a tomar
- Calcular el discounted rewards usando como línea de base la media estandardizada del retorno $$ \frac{x_i - \bar{x}}{\sigma_x}$$
- Calcular la media de recompensas de los últimos 100 episodios
- Implementar la pérdida por actualización
- Las recompensas obtenidas en cada paso del entrenamiento
- Las recompensas medias de los 100 episodios anteriores
- La pérdida durante el entrenamiento
import statistics
class reinforceAgent:
###################################################
######TODO 1: declarar variables ##################
def __init__(self, env, dnnetwork):
"""
Params
======
env: entorno
dnnetwork: clase con la red neuronal diseñada
nblock: bloque de los X últimos episodios de los que se calculará la media de recompensa
reward_threshold: umbral de recompensa definido en el entorno
"""
self.env = env
self.dnnetwork = dnnetwork
#self.dnnetwork = None
#self.nblock = None
self.nblock = 100
#self.reward_threshold = None
self.reward_threshold =self.env.spec.reward_threshold
self.initialize()
###############################################################
#####TODO 2: inicializar variables extra que se necesiten######:
def initialize(self):
self.batch_rewards = []
self.batch_actions = []
self.batch_states = []
self.batch_counter = 1
#mio
self.sync_eps = []
self.total_reward = 0
self.step_count = 0
self.state0 = self.env.reset()
self.update_loss = []
self.training_rewards = []
self.mean_training_rewards = []
#mio para epsiolons y loss
self.epsilon_conteo = []
self.loss_conteo = []
## Entrenamiento
def train(self, gamma=0.99, max_episodes=2000, batch_size=10):
self.gamma = gamma
self.batch_size = batch_size
episode = 0
action_space = np.arange(self.env.action_space.n)
training = True
print("Training...")
while training:
state0 = env.reset()
episode_states = []
episode_rewards = []
episode_actions = []
gamedone = False
while gamedone == False:
###########################################################
######TODO 3: Tomar nueva acción ##############################################
#action_probs = None #distribución de probabilidad de las acciones dado el estado actual
#action = None #acción aleatoria de la distribución de probabilidad
action_probs = self.dnnetwork.get_action_prob(state0).detach().numpy()
action = np.random.choice(action_space, p=action_probs)
#next_state, reward, gamedone, _ = None
next_state, reward, gamedone, _ = env.step(action)
##########
# Almacenamos experiencias que se van obteniendo en este episodio
episode_states.append(state0)
episode_rewards.append(reward)
episode_actions.append(action)
state0 = next_state
if gamedone:
episode += 1
# Calculamos el término del retorno menos la línea de base
self.batch_rewards.extend(self.discount_rewards(episode_rewards))
self.batch_states.extend(episode_states)
self.batch_actions.extend(episode_actions)
self.batch_counter += 1
#####################################################################################
###TODO 5: calcular media de recompensas de los últimos X episodios, y almacenar#####
self.training_rewards.append(sum(episode_rewards)) # guardamos las recompensas obtenidas
mean_rewards = np.mean(self.training_rewards[-self.nblock:])
self.mean_training_rewards.append(mean_rewards)
#mean_rewards = None
######
# Actualizamos la red cuando se completa el tamaño del batch
if self.batch_counter == self.batch_size:
self.update(self.batch_states, self.batch_rewards, self.batch_actions)
self.loss_conteo.append(self.update_loss) #NUEVO
self.update_loss = []
# Reseteamos las variables del epsiodio
self.batch_rewards = []
self.batch_actions = []
self.batch_states = []
self.batch_counter = 1
print("\rEpisode {:d} Mean Rewards {:.2f}\t\t".format(
episode, mean_rewards), end="")
# Comprobamos que todavía quedan episodios
if episode >= max_episodes:
training = False
print('\nEpisode limit reached.')
break
# Termina el juego si la media de recompensas ha llegado al umbral fijado para este juego
if mean_rewards >= self.reward_threshold:
training = False
print('\nEnvironment solved in {} episodes!'.format(
episode))
break
######################################################
###TODO 4: cálculo del retorno menos la línea de base###
def discount_rewards(self, rewards):
discount_r = np.zeros_like(rewards)
timesteps = range(len(rewards))
reward_sum = 0
for i in reversed(timesteps):
reward_sum = rewards[i] + self.gamma*reward_sum
discount_r[i] = reward_sum
#mio
baseline = 0
#for i in reversed(timesteps):
a = np.array(discount_r)
baseline = discount_r.mean()/statistics.stdev(a)
#baseline = None
return discount_r - baseline
########
#Actualización
def update(self, batch_s, batch_r, batch_a):
self.dnnetwork.optimizer.zero_grad() # eliminamos cualquier gradiente pasado
state_t = torch.FloatTensor(batch_s)
reward_t = torch.FloatTensor(batch_r)
action_t = torch.LongTensor(batch_a)
loss = self.calculate_loss(state_t, action_t, reward_t) # calculamos la pérdida
loss.backward() # hacemos la diferencia para obtener los gradientes
self.dnnetwork.optimizer.step() # aplicamos los gradientes a la red neuronal
# Guardamos los valores de pérdida
if self.dnnetwork.device == 'cuda':
self.update_loss.append(loss.detach().cpu().numpy())
else:
self.update_loss.append(loss.detach().numpy())
###########################################
###TODO 6: Cálculo de la pérdida###########
# Recordatorio: cada actualización es proporcional al producto del retorno y el gradiente de la probabilidad
# de tomar la acción tomada, dividido por la probabilidad de tomar esa acción (logaritmo natural)
def calculate_loss(self, state_t, action_t, reward_t):
logprob = torch.log(self.dnnetwork.get_action_prob(state_t))
selected_logprobs = reward_t * \
logprob[np.arange(len(action_t)), action_t]
loss = -selected_logprobs.mean()
return loss
#logprob = None
#selected_logprobs = None
#loss = None
#return loss
#######
def plot_rewards(self):
plt.figure(figsize=(12,8))
plt.plot(self.training_rewards, label='Rewards')
plt.plot(self.mean_training_rewards, label='Mean Rewards')
plt.axhline(self.reward_threshold, color='r', label="Reward threshold")
plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.legend(loc="upper left")
plt.show()
def plot_loss(self):
plt.figure(figsize=(12,8))
plt.plot(self.loss_conteo, label='Rewards')
plt.xlabel('Episodes')
plt.ylabel('loss')
plt.legend(loc="upper left")
plt.show()
#store
def save(self, step, logs_path):
os.makedirs(logs_path, exist_ok=True)
model_list = glob.glob(os.path.join(logs_path, '*.pth'))
logs_path = os.path.join(logs_path, 'model-{
}.pth' .format(step))
self.dnnetwork.save(logs_path, step=step, optimizer=self.dnnetwork.optimizer)
print('=> Save {
}' .format(logs_path))
def restore(self, logs_path):
self.dnnetwork.load(logs_path)
print('=> Restore {}' .format(logs_path))
4.3 Entrenamiento
A continuación entrenaremos el modelo con los siguientes hiperparámetros:
- Velocidad de aprendizaje: 0.005
- Tamaño del batch: 8
- Gamma: 0.99
- Número máximo de episodios: 5000
Definir los hiperparámetros, cargar el modelo de red neuronal y entrenar el agente ------------------------------------------------------------------------------------------ Nota: este modelo puede tardar más de 50 minutos en ejecutarse.
lr = 0.005 #Velocidad aprendizaje
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 8 #Conjunto a coger del buffer para la red neuronal
MAX_EPISODES = 5000 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000 #Frecuencia de sincronización de pesos entre red neuronal y red objetivo
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('Cargamos el modelo de red neuronal:')
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
env = gym.make('LunarLander-v2')
PGReinforce = PGReinforce(env,lr)
print('Creamos nuestro agente:')
agent = reinforceAgent(env, PGReinforce)
print('Entrenamos el agente con los hiperparámetros establecidos:')
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE)
agent_PGReinforce = deepcopy(agent)
Cargamos el modelo de red neuronal: Creamos nuestro agente: Entrenamos el agente con los hiperparámetros establecidos: Training... Episode 3550 Mean Rewards 200.26 Environment solved in 3550 episodes!
Mostrar los siguientes gráficos:
- Recompensas obtenidas a lo largo del entrenamieno y la evolución de las recompensas medias cada 100 episodios, junto con el umbral de recompensa establecido por el entorno
- Pérdida durante el entrenamiento
agent.plot_rewards()
agent.plot_loss()
Análisis: Guardar el modelo entrenado en formato ".pth" y comentar los resultados obtenidos. ¿Qué ha ocurrido con este modelo?
import os
agent.save('','ModeloreinforceAgent')
agent.restore('ModeloreinforceAgent/model-.pth')
=> Save ModeloreinforceAgent/model-.pth => Restore ModeloreinforceAgent/model-.pth
Análisis
Este agente a tenido un proceso de entrenamiento más costoso que el resto de ejemplos análizados. No poder actualizar la apolítica hasta el final de cada episodio hace que el aprendizaje sea mucho más lento que con las DQN.
4.4 Test del agente
Cargar el modelo entrenado y ejecutar el agente entrenado durante 100 episodios consecutivos. Calcular la suma de recompensas por cada episodio. Mostrar en un gráfico la suma de las recompensas respecto de los episodios, incluyendo el umbral de recompensa establecido por el entorno. Comentar los resultados. --------------------------------------------------------------------------------------------------- Opcional: visualizar los episodios con
env.render(), sólo posible en local. Esta visualización ralentiza el proceso unos segundos por episodio. import base64
def show_video(iteration):
mp4list = glob.glob('videoreinforceAgent/'+str(iteration)+'/*.mp4')
if len(mp4list) > 0:
mp4 = mp4list[0]
video = io.open(mp4, 'r+b').read()
encoded = base64.b64encode(video)
ipythondisplay.display(HTML(data='''<video alt="test" autoplay
loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>'''.format(encoded.decode('ascii'))))
else:
print("Could not find video")
def wrap_env(env, iteration):
env = Monitor(env, './videoreinforceAgent/'+str(iteration)+'/', force=True)
return env
num_episodes = 100 # number of episodes
max_steps_ep = 10000 # default max number of steps per episode (unless env has a lower hardcoded limit)
numero_pasos = []
umbral_recompensa = []
scores = []
actions = range(env.action_space.n)
for i in tqdm(range(1, num_episodes+1)):
env = gym.make('LunarLander-v2')
max_episodios_entorno = env._max_episode_steps
umbral_recompensa.append(env.spec.reward_threshold)
env = wrap_env(env,i)
state = env.reset()
score = 0
max_steps_ep = 0
while max_steps_ep< max_episodios_entorno:
max_steps_ep= max_steps_ep +1
action =np.random.choice(actions, p=agent.dnnetwork.get_action_prob(state).detach().numpy())
state, reward, done, info = env.step(action)
score += reward
if done:
break
if not done:
env.stats_recorder.save_complete()
env.stats_recorder.done = True
env.close()
#print('Episode {}, score: {}'.format(i, score))
scores.append(score)
numero_pasos.append(max_steps_ep)
show_video(i)
100%|██████████| 100/100 [47:43<00:00, 28.63s/it]
plt.figure(figsize=(12,8))
plt.plot(scores, label='Rewards')
plt.axhline(200, color='r', label="Reward threshold")
plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.legend(loc="upper left")
plt.show()
plt.xlabel('Recompensa')
plt.ylabel('Cantidad')
plt.title('Histograma con la suma de recompensas de cada episodio')
plt.grid(True)
plt.axvline(200, color='k', linestyle='dashed', linewidth=2)
plt.hist(scores, bins =40)
plt.axis([0, 350, 0, 20])
plt.show()
score_PGReinforce = deepcopy(scores)
Análisis
Los resultados obtenidos no han sido los mejores. Realmente me he encontrado ante una solución con una tasa de exito menor que el resto de los agentes debido a la variabilidad del juego y cono esta ha afectado al agente estudiado. El modelo no tiene tanta capacidad de aprendizaje del entorno y eso provoca que no pueda adaptarse tan bien a los pequeños cambios como el resto de algoritmos.
Por todo ello, reinforce ha obtenido la peor tasa de exito con un entrenamiento muy costos que no ha proporcionado los resultado deseados.
5. Comparación de modelos (1 pto)
Ejercicio: Muestra en un mismo gráfico la evolución de la media de recompensas de los tres modelos, junto con el umbral de recompensa.
plt.figure(figsize=(12,8))
plt.plot(agent_DDQN.mean_training_rewards, label='RewardsDDQN')
plt.plot(agent_duelingDQN.mean_training_rewards, label='duelingDQN ')
plt.plot(agent_PGReinforce.mean_training_rewards, label='PGReinforce')
plt.axhline(200, color='r', label="Reward threshold")
plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.legend(loc="upper left")
plt.show()
num_episodes = 100 # number of episodes
max_steps_ep = 10000 # default max number of steps per episode (unless env has a lower hardcoded limit)
numero_pasos = []
umbral_recompensa = []
scores = []
actions = range(env.action_space.n)
for i in tqdm(range(1, num_episodes+1)):
env = gym.make('LunarLander-v2')
max_episodios_entorno = env._max_episode_steps
umbral_recompensa.append(env.spec.reward_threshold)
#env = wrap_env(env,i)
state = env.reset()
score = 0
max_steps_ep = 0
while max_steps_ep< max_episodios_entorno:
max_steps_ep= max_steps_ep +1
action = agent_DDQN.dnnetwork.get_action(state,agent_DDQN.epsilon)
state, reward, done, info = env.step(action)
score += reward
if done:
break
if not done:
env.stats_recorder.save_complete()
env.stats_recorder.done = True
env.close()
#print('Episode {}, score: {}'.format(i, score))
scores.append(score)
numero_pasos.append(max_steps_ep)
#show_video(i)
score_DDQN = deepcopy(scores)
num_episodes = 100 # number of episodes
max_steps_ep = 10000 # default max number of steps per episode (unless env has a lower hardcoded limit)
numero_pasos = []
umbral_recompensa = []
scores = []
actions = range(env.action_space.n)
for i in tqdm(range(1, num_episodes+1)):
env = gym.make('LunarLander-v2')
max_episodios_entorno = env._max_episode_steps
umbral_recompensa.append(env.spec.reward_threshold)
#env = wrap_env(env,i)
state = env.reset()
score = 0
max_steps_ep = 0
while max_steps_ep< max_episodios_entorno:
max_steps_ep= max_steps_ep +1
action = agent_duelingDQN.dnnetwork.get_action(state,agent_duelingDQN.epsilon)
state, reward, done, info = env.step(action)
score += reward
if done:
break
if not done:
env.stats_recorder.save_complete()
env.stats_recorder.done = True
env.close()
#print('Episode {}, score: {}'.format(i, score))
scores.append(score)
numero_pasos.append(max_steps_ep)
#show_video(i)
score_duelingDQN = deepcopy(scores)
100%|██████████| 100/100 [00:28<00:00, 3.57it/s] 100%|██████████| 100/100 [00:26<00:00, 3.78it/s]
plt.figure(figsize=(12,8))
plt.plot(score_DDQN, label='RewardsDDQN')
plt.plot(score_duelingDQN, label='duelingDQN ')
plt.plot(score_PGReinforce, label='PGReinforce')
plt.axhline(200, color='r', label="Reward threshold")
plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.legend(loc="upper left")
plt.show()
plt.xlabel('Recompensa')
plt.ylabel('Cantidad')
plt.title('Histograma con la suma de recompensas de cada episodio')
plt.grid(True)
plt.axvline(200, color='k', linestyle='dashed', linewidth=2)
plt.hist(score_DDQN, bins =40, alpha=0.3, label='score_DDQN ')
plt.hist(score_duelingDQN, bins =40, alpha=0.3, label='duelingDQN ')
plt.hist(score_PGReinforce, bins =40, alpha=0.3, label='PGReinforce ')
plt.legend(loc="upper left")
plt.axis([0, 350, 0, 20])
plt.show()
score_PGReinforce = deepcopy(scores)
Análisis: Analizar los resultados obtenidos teniendo en cuenta el número de episodios, el tiempo de entrenamiento y el rendimiento de los tres agentes entrenados observado en apartados anteriores. ¿Qué agente presenta un mejor comportamiento? ¿Por qué?
Análisis
DuelingDQN ha tenido un mejor resultado, seguido de DDQN y para acabar el PGReinforce.
Esto es debido al tipo de entorno. A pesar de que añadiendo una línea de base para reducir la variabilidad, PGReinforce creo que no se adapta tan bien a la variabilidad.
Los otros dos algoritmos han obtenido muy buenos resultados. En el algoritmo DDQN la red neuronal principal decide cuál es la mejor acción entre todas las posibles, y luego la red objetivo evalúa esa acción para conocer su valor-Q.
Esta solución ha dado muy buenos resultado pero realmente los mejores resultados los hemos obtenido con el algoritmo Dueling DQN. Este algoritmo ha dividido su capa final en dos, una para estimar el valor del estado s (V(s)) y otra para estimar la ventaja de cada acción a (A(s, a)), y al final juntar ambas partes en una sola, la cual estimará los valores-Q. Este cambio ayuda, porque a veces no es necesario saber exactamente al valor de cada acción, por lo que aprender el valor del estado puede ser suficiente. Este hecho permite aprender más al agente y proporcionar mejores resultados.
6. Optimización
En este apartado queremos encontrar la mejor arquitectura e hiperparámetros para optimizar la precisión del modelo. Los puntos que queremos tener en cuenta para la búsqueda del mejor modelo son los siguientes:
- Número de unidades de las capas
- Learning rate
- Actualización de la red principal
- Sincronización de la red objetivo
- Batch size
- Gamma
No evaluable -< Código para obtener la tabla comparativa.
print('------------------------')
print('Blucle de la subdivision y multiplicación')
print('------------------------')
lr = 25*10**(-5) #Velocidad aprendizaje
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
MAX_EPISODES = 350 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 32 #Conjunto a coger del buffer para la red neuronal
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000 #Frecuencia de sincronización de pesos entre red neuronal y red objetivo
print('Inicio')
for i in [#0.25,0.5,
2,4
]:
print('---------------------------------------')
print(i)
print('---------------------------------------')
print('lr')
env = gym.make('LunarLander-v2')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
lr = lr* i
ddqn = DDQN(n_inputs,n_outputs, lr, np.arange(env.action_space.n))
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
#
#
#
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('DNN_UPD')
lr = 25*10**(-5)
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN(n_inputs,n_outputs, lr, np.arange(env.action_space.n))
#duelingDQN = duelingDQN(env,lr)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
DNN_UPD = DNN_UPD* i
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
#
#
#
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('BATCH_SIZE')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN(n_inputs,n_outputs, lr, np.arange(env.action_space.n))
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
BATCH_SIZE = BATCH_SIZE* i
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
#
#
#
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('GAMMA')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN(n_inputs,n_outputs, lr, np.arange(env.action_space.n))
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
BATCH_SIZE = 32 #Conjunto a coger del buffer para la red neuronal
if i>=1:
GAMMA = GAMMA* i
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
#
#
print('DNN_SYNC')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN(n_inputs,n_outputs, lr, np.arange(env.action_space.n))
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
DNN_SYNC = DNN_SYNC* i
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
DNN_SYNC = 1000 #Frecuencia de sincronización de pesos entre red neuronal y red objetivo
print('DNN_SYNC')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN(n_inputs,n_outputs, lr, np.arange(env.action_space.n))
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
DNN_SYNC = DNN_SYNC* 0.25
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
DNN_SYNC = 1000 #Frecuencia de sincronización de pesos entre red neuronal y red objetivo
print('BATCH_SIZE')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN(n_inputs,n_outputs, lr, np.arange(env.action_space.n))
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
BATCH_SIZE = BATCH_SIZE* 0.25
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
------------------------ Blucle de la subdivision y multiplicación ------------------------ Inicio --------------------------------------- 2 --------------------------------------- lr Filling replay buffer... Training...
<ipython-input-15-07c6c18ad12e>:187: UserWarning: indexing with dtype torch.uint8 is now deprecated, please use a dtype torch.bool instead. (Triggered internally at ../aten/src/ATen/native/IndexingUtils.h:25.) qvals_next[dones_t] = 0
Episode 350 Mean Rewards 153.84 Epsilon 0.029969735809067772 Episode limit reached. DNN_UPD Filling replay buffer... Training... Episode 350 Mean Rewards -57.36 Epsilon 0.029969735809067772 Episode limit reached. BATCH_SIZE Filling replay buffer... Training... Episode 350 Mean Rewards 76.23 Epsilon 0.029969735809067772 Episode limit reached. GAMMA Filling replay buffer... Training... Episode 350 Mean Rewards -351.65 Epsilon 0.029969735809067772 Episode limit reached. DNN_SYNC Filling replay buffer... Training... Episode 350 Mean Rewards 162.48 Epsilon 0.029969735809067772 Episode limit reached. --------------------------------------- 4 --------------------------------------- lr Filling replay buffer... Training... Episode 350 Mean Rewards 151.36 Epsilon 0.029969735809067772 Episode limit reached. DNN_UPD Filling replay buffer... Training... Episode 350 Mean Rewards -273.40 Epsilon 0.029969735809067772 Episode limit reached. BATCH_SIZE Filling replay buffer... Training... Episode 350 Mean Rewards 92.20 Epsilon 0.029969735809067772 Episode limit reached. GAMMA Filling replay buffer... Training... Episode 350 Mean Rewards -557.03 Epsilon 0.029969735809067772 Episode limit reached. DNN_SYNC Filling replay buffer... Training... Episode 350 Mean Rewards -45.13 Epsilon 0.029969735809067772 Episode limit reached. DNN_SYNC Filling replay buffer... Training... Episode 350 Mean Rewards -12.57 Epsilon 0.029969735809067772 Episode limit reached. BATCH_SIZE Filling replay buffer... Training... Episode 350 Mean Rewards 78.72 Epsilon 0.029969735809067772 Episode limit reached.
class duelingDQN_2(torch.nn.Module):
def __init__(self, env,lr, num_multi ,device='cpu'):
"""
Params
======
n_inputs: tamaño del espacio de estadps
n_outputs: tamaño del espacio de acciones
actions: array de acciones posibles
"""
super(duelingDQN_2, self).__init__()
self.device = device
self.n_inputs = env.observation_space.shape[0]
self.n_outputs = env.action_space.n
self.actions = np.arange(env.action_space.n)
self.fc = torch.nn.Linear(self.n_inputs, int(256*num_multi), bias=True)
self.fc2 = torch.nn.Linear(int(256*num_multi), int(128*num_multi), bias=True)
# Sub-red de la función de Valor
self.fc_v1 = torch.nn.Linear(int(128*num_multi), int(64*num_multi), bias=True)
self.fc_v = torch.nn.Linear(int(64*num_multi), self.n_outputs, bias=True)
'''
self.fc_v = torch.nn.Sequential(
torch.nn.Linear(128, 64, bias=True),
torch.nn.ReLU(),
torch.nn.Linear(64, self.n_outputs, bias=True)
)
'''
# Sub-red de la Ventaja A(s,a)
self.fc_advantage1= torch.nn.Linear(int(128*num_multi), int(64*num_multi), bias=True)
self.fc_advantage= torch.nn.Linear(int(64*num_multi), 1, bias=True)
'''
self.fc_advantage = torch.nn.Sequential(
torch.nn.Linear(128, 64, bias=True),
torch.nn.ReLU(),
torch.nn.Linear(64, 1, bias=True)
)
'''
self.optimizer = torch.optim.Adam(self.parameters(), lr=lr)
#######################################
#####TODO: función forward#############
def forward(self, state):
'''
out = self.head(x)
val_out = self.val(out).reshape(out.shape[0], 1)
adv_out = self.adv(out).reshape(out.shape[0], -1)
adv_mean = adv_out.mean(dim=1, keepdim=True)
q = val_out + adv_out - adv_mean
'''
#return q
#Conexión entre capas Red común
x = torch.nn.functional.relu(self.fc(state))
x = self.fc2(x)
x = torch.nn.functional.relu(x)
#Conexión entre capas Sub-red Valor
val_out1 = torch.nn.functional.relu(self.fc_v1(x))#.reshape(out.shape[0], 1)
val_out = self.fc_v(val_out1)
'''
val_out = self.fc_v(x)
'''
#Conexión entre capas Sub-red Ventaja
'''
adv = self.fc_advantage(x)#.reshape(out.shape[0], -1)
'''
adv = torch.nn.functional.relu(self.fc_advantage1(x))
adv = self.fc_advantage(adv)
#Agregar las dos subredes: Q(s,a) = V(s) + (A(s,a) - 1/|A| * sum A(s,a'))
#action = None
action = val_out + (adv - adv.mean())
return action
if self.device == 'cuda':
self.model.cuda()
### Método e-greedy
def get_action(self, state, epsilon=0.05):
if np.random.random() < epsilon:
action = np.random.choice(self.actions)
else:
qvals = self.get_qvals(state)
action= torch.max(qvals, dim=-1)[1].item()
return action
def get_qvals(self, state):
if type(state) is tuple:
state = np.array([np.ravel(s) for s in state])
state_t = torch.FloatTensor(state).to(device=self.device)
return self.forward(state_t)
def save(self, path, step, optimizer):
torch.save({
'step': step,
'state_dict': self.state_dict(),
'optimizer': optimizer.state_dict()
}, path)
def load(self, checkpoint_path, optimizer=None):
checkpoint = torch.load(checkpoint_path)
step = checkpoint['step']
self.load_state_dict(checkpoint['state_dict'])
if optimizer is not None:
optimizer.load_state_dict(checkpoint['optimizer'])
class DDQN_2(torch.nn.Module):
def __init__(self, n_inputs, n_outputs, learning_rate, actions , num_multi,device='cpu'):
"""
Params
======
n_inputs: tamaño del espacio de estadps
n_outputs: tamaño del espacio de acciones
actions: array de acciones posibles
"""
super(DDQN_2, self).__init__()
self.device = device
self.actions = actions
self.learning_rate = learning_rate
self.n_inputs = n_inputs
self.n_outputs = n_outputs
self.model = torch.nn.Sequential(
torch.nn.Linear(self.n_inputs, int(256*num_multi), bias=True),
torch.nn.ReLU(),
torch.nn.Linear(int(256*num_multi), int(128*num_multi), bias=True),
torch.nn.ReLU(),
torch.nn.Linear(int(128*num_multi), int(64*num_multi), bias=True),
torch.nn.ReLU(),
torch.nn.Linear(int(64*num_multi), self.n_outputs, bias=True))
self.optimizer = None
self.optimizer = torch.optim.Adam(self.parameters(), lr=self.learning_rate)
if self.device == 'cuda':
self.model.cuda()
### Método e-greedy
def get_action(self, state, epsilon=0.05):
if np.random.random() < epsilon:
action = np.random.choice(self.actions)
else:
qvals = self.get_qvals(state)
action= torch.max(qvals, dim=-1)[1].item()
return action
def get_qvals(self, state):
if type(state) is tuple:
state = np.array([np.ravel(s) for s in state])
state_t = torch.FloatTensor(state).to(device=self.device)
return self.model(state_t)
def save(self, path, step, optimizer):
torch.save({
'step': step,
'state_dict': self.state_dict(),
'optimizer': optimizer.state_dict()
}, path)
def load(self, checkpoint_path, optimizer=None):
checkpoint = torch.load(checkpoint_path)
step = checkpoint['step']
self.load_state_dict(checkpoint['state_dict'])
if optimizer is not None:
optimizer.load_state_dict(checkpoint['optimizer'])
print('------------------------')
print('Multiplicación capas')
print('------------------------')
lr = 25*10**(-5) #Velocidad aprendizaje
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
MAX_EPISODES = 350 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 32 #Conjunto a coger del buffer para la red neuronal
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000 #Frecuencia de sincronización de pesos entre red neuronal y red objetivo
print('Inicio')
for num_multi in [0.5]:
print('---------------------------------------')
print('Neuronas con un valor: ' + str(num_multi))
print('---------------------------------------')
print('---------------------------------------')
for i in [1,2,0.5]:
print('---------------------------------------')
print(i)
print('---------------------------------------')
print('lr')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
lr = lr* i
ddqn = DDQN_2(n_inputs,n_outputs, lr, np.arange(env.action_space.n),num_multi)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr,num_multi)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
#
#
#
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('DNN_UPD')
lr = 25*10**(-5)
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN_2(n_inputs,n_outputs, lr, np.arange(env.action_space.n),num_multi)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr,num_multi)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
DNN_UPD = DNN_UPD* i
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
#
#
#
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('BATCH_SIZE')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN_2(n_inputs,n_outputs, lr, np.arange(env.action_space.n),num_multi)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr,num_multi)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
BATCH_SIZE = BATCH_SIZE* i
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
#
#
#
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
print('GAMMA')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN_2(n_inputs,n_outputs, lr, np.arange(env.action_space.n),num_multi)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr,num_multi)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
BATCH_SIZE = 32 #Conjunto a coger del buffer para la red neuronal
if i>=1:
GAMMA = GAMMA* i
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
#
#
#
print('DNN_SYNC')
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN_2(n_inputs,n_outputs, lr, np.arange(env.action_space.n),num_multi)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
#duelingDQN = duelingDQN(env,lr,num_multi)
#agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
DNN_SYNC = DNN_SYNC* i
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
DNN_SYNC = 1000 #Frecuencia de sincronización de pesos entre red neuronal y red objetivo
------------------------ Multiplicación capas ------------------------ Inicio --------------------------------------- Neuronas con un valor: 0.5 --------------------------------------- --------------------------------------- --------------------------------------- 1 --------------------------------------- lr Filling replay buffer... Training... Episode 2 Mean Rewards -92.18 Epsilon 0.99
<ipython-input-15-07c6c18ad12e>:187: UserWarning: indexing with dtype torch.uint8 is now deprecated, please use a dtype torch.bool instead. (Triggered internally at ../aten/src/ATen/native/IndexingUtils.h:25.) qvals_next[dones_t] = 0
Episode 350 Mean Rewards -60.68 Epsilon 0.029969735809067772 Episode limit reached. DNN_UPD Filling replay buffer... Training... Episode 350 Mean Rewards -183.19 Epsilon 0.029969735809067772 Episode limit reached. BATCH_SIZE Filling replay buffer... Training... Episode 350 Mean Rewards -134.57 Epsilon 0.029969735809067772 Episode limit reached. GAMMA Filling replay buffer... Training... Episode 350 Mean Rewards -60.32 Epsilon 0.029969735809067772 Episode limit reached. DNN_SYNC Filling replay buffer... Training... Episode 350 Mean Rewards -139.96 Epsilon 0.029969735809067772 Episode limit reached. --------------------------------------- 2 --------------------------------------- lr Filling replay buffer... Training... Episode 350 Mean Rewards -65.71 Epsilon 0.029969735809067772 Episode limit reached. DNN_UPD Filling replay buffer... Training... Episode 350 Mean Rewards -300.00 Epsilon 0.029969735809067772 Episode limit reached. BATCH_SIZE Filling replay buffer... Training... Episode 350 Mean Rewards -110.17 Epsilon 0.029969735809067772 Episode limit reached. GAMMA Filling replay buffer... Training... Episode 350 Mean Rewards -510.71 Epsilon 0.029969735809067772 Episode limit reached. DNN_SYNC Filling replay buffer... Training... Episode 350 Mean Rewards -18.52 Epsilon 0.029969735809067772 Episode limit reached. --------------------------------------- 0.5 --------------------------------------- lr Filling replay buffer... Training... Episode 350 Mean Rewards -138.59 Epsilon 0.029969735809067772 Episode limit reached. DNN_UPD Filling replay buffer... Training... Episode 350 Mean Rewards -87.53 Epsilon 0.029969735809067772 Episode limit reached. BATCH_SIZE Filling replay buffer... Training... Episode 350 Mean Rewards -118.28 Epsilon 0.029969735809067772 Episode limit reached. GAMMA DNN_SYNC Filling replay buffer... Training... Episode 350 Mean Rewards -39.80 Epsilon 0.029969735809067772 Episode limit reached.
Ejercicio: Elegir uno de los dos modelos de DQN implementados (DDQN o dueling DQN) y experimentar con diferentes combinaciones de valores para los parámetros especificados. El objetivo es conseguir un modelo con el que el agente tarde menos de 350 episodios en resolver el entorno. Indicar las pruebas realizadas, pero presentar únicamente la ejecución y resultados de la mejor opción.
Análisis
| Multiplicación Valor Inicial | lr | DNN_UPD | BATCH_SIZE | GAMMA | DNN_SYNC | Cantida de neuronas |
|---|---|---|---|---|---|---|
| 0.25 | 350/-155.87 | 350/98.08 | 350/78.72 | - | 350/-12.57 | Inicial |
| 0.5 | 350/-18.51 | 350/-50.82 | 350/-41.9 | - | 350/56.33 | Inicial |
| 2 | 350/153.84 | 350/ -57.36 | 350/76.23 | 350/-351.65 | 350/162.48 | Inicial |
| 4 | 350/151.36 | 350/-273.40 | 350/92.20 | 350/-557.03 | 350/-45.13 | Inicial |
| Multiplicación Valor Inicial | lr | DNN_UPD | BATCH_SIZE | GAMMA | DNN_SYNC | Cantida de neuronas |
|---|---|---|---|---|---|---|
| 0.5 | 350/-4.07 | 350/36.05 | 350/158.08 | - | 350/180.21 | Inicial * 2 |
| 1 | 350/149.88 | 350/97.72 | 337/200.81 | 350/73.44 | 350/ 60.07 | Inicial *2 |
| 2 | 350/101.48 | 350/-98.67 | 350/132.58 | 350/-396.62 | 350/22.94 | Inicial * 2 |
| Multiplicación Valor Inicial | lr | DNN_UPD | BATCH_SIZE | GAMMA | DNN_SYNC | Cantida de neuronas |
|---|---|---|---|---|---|---|
| 0.5 | 350/-138.59 | 350/-87.53 | 350/118.28 | - | 350/-39.80 | Inicial * 0.5 |
| 1 | 350/-60.68 | 350/-183.19 | 350/-134.57 | 350/-60.32 | 350/-139.96 | Inicial * 0.5 |
| 2 | 350/-65.71 | 350/-300.00 | 337/-110.17 | 350/-510.71 | 350/ -18.52 | Inicial * 0.5 |
Elaboración de la tabla
Estas tablas contienen la inforamción de los diferentes test que he realizado para conocer como afectada cada uno de los parámetros por separado.
He decidido utilizar la opción más costosa, es decir, el algoritmo menos eficiente (DDQN) para poder valorar correctamente el peso de cada carácteristica.
En cada una de las tablas, he introducido la columna Multiplicación Valor Inicial que es el valor por el que he multiplicado los diferentes componente, es decir, Número de unidades de las capas, Learning rate , Actualización de la red principal, Sincronización de la red objetivo, Batch size y Gamma.
También he reimplementado los módelos para que se pudiera añadir una variable entera que multiplique la cantidad de neuronas por capa respecti a la inicial indicada en el enunciado.
Análisis: Justificar los valores elegidos de hiperparámetros para las distintas pruebas realizadas y comentar los resultados de entrenamiento y de rendimiento del agente entrenado.
lr = 25*10**(-5) * 1 #Velocidad aprendizaje
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
MAX_EPISODES = 350 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 32 * 3 #Conjunto a coger del buffer para la red neuronal
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN_2(n_inputs,n_outputs, lr, np.arange(env.action_space.n), 2)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
Filling replay buffer... Training...
<ipython-input-15-07c6c18ad12e>:187: UserWarning: indexing with dtype torch.uint8 is now deprecated, please use a dtype torch.bool instead. (Triggered internally at ../aten/src/ATen/native/IndexingUtils.h:25.) qvals_next[dones_t] = 0
Episode 267 Mean Rewards 200.13 Epsilon 0.06901790349970886 Environment solved in 267 episodes!
lr = 25*10**(-5) * 1 #Velocidad aprendizaje
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
MAX_EPISODES = 350 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 32 * 3 #Conjunto a coger del buffer para la red neuronal
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN_2(n_inputs,n_outputs, lr, np.arange(env.action_space.n), 2)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
Filling replay buffer... Training... Episode 1 Mean Rewards -68.49 Epsilon 1
<ipython-input-15-07c6c18ad12e>:187: UserWarning: indexing with dtype torch.uint8 is now deprecated, please use a dtype torch.bool instead. (Triggered internally at ../aten/src/ATen/native/IndexingUtils.h:25.) qvals_next[dones_t] = 0
Episode 317 Mean Rewards 201.23 Epsilon 0.04175625035843686 Environment solved in 317 episodes!
lr = 25*10**(-5) * 1 #Velocidad aprendizaje
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
MAX_EPISODES = 350 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 32 * 3 #Conjunto a coger del buffer para la red neuronal
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
ddqn = DDQN_2(n_inputs,n_outputs, lr, np.arange(env.action_space.n), 2)
agent = DDQNAgent(env, ddqn, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE)
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
agent.plot_rewards()
Filling replay buffer... Training...
<ipython-input-14-07c6c18ad12e>:187: UserWarning: indexing with dtype torch.uint8 is now deprecated, please use a dtype torch.bool instead. (Triggered internally at ../aten/src/ATen/native/IndexingUtils.h:25.) qvals_next[dones_t] = 0
Episode 265 Mean Rewards 200.43 Epsilon 0.07041924650516158 Environment solved in 265 episodes!
lr = 25*10**(-5) * 1 #Velocidad aprendizaje
MEMORY_SIZE = 10000 #Máxima capacidad del buffer
MAX_EPISODES = 350 #Número máximo de episodios (el agente debe aprender antes de llegar a este valor)
EPSILON = 1 #Valor inicial de epsilon
EPSILON_DECAY = .99 #Decaimiento de epsilon
GAMMA = 0.99 #Valor gamma de la ecuación de Bellman
BATCH_SIZE = 32 * 3 #Conjunto a coger del buffer para la red neuronal
BURN_IN = 1000 #Número de episodios iniciales usados para rellenar el buffer antes de entrenar
DNN_UPD = 5 #Frecuencia de actualización de la red neuronal
DNN_SYNC = 1000
buffer = experienceReplayBuffer(memory_size=MEMORY_SIZE, burn_in=BURN_IN)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
duelingDQN = duelingDQN_2(env,lr,2)
agent = duelingDQNAgent(env, duelingDQN, buffer, EPSILON, EPSILON_DECAY, BATCH_SIZE, lr)
agent.train(gamma=GAMMA, max_episodes=MAX_EPISODES,
batch_size=BATCH_SIZE, dnn_update_frequency=DNN_UPD,
dnn_sync_frequency=DNN_SYNC)
Filling replay buffer... Training...
<ipython-input-39-bd3d70f337a8>:191: UserWarning: indexing with dtype torch.uint8 is now deprecated, please use a dtype torch.bool instead. (Triggered internally at ../aten/src/ATen/native/IndexingUtils.h:25.) qvals_next[dones_t] = 0
Episode 275 Mean Rewards 200.47 Epsilon 0.06368590427489453 Environment solved in 275 episodes!
agent.plot_rewards()
La configuración optima ha sido
- Número de unidades de las capas: Multiplicar por 2
- Learning rate = 25*10**(-5)
- Actualización de la red principal: 5
- Sincronización de la red objetivo: 1000
- Batch size: Multiplicar por 3
- Gamma:0.99
De la tabla comparativa, he obtenido mucha información. He observado que, en cierta medida, aumentar el doble de Conjunto a coger del buffer para la red neuronal y el Número de unidades de las capas suponía una aumento en la recompensa.
A partir de esa teoría, he realizado dos ejecuciones con el modelo DDQN dónde he obtenido un modelo entrenado en 267y 317 episodios. Esto es debido a que he aumentado la capacidad de aprendizaje del algoritmo y puede conocer más por episodio.
Una vez comprobado, he analizado si esta teoría era aplicable al modelo dueling DQN. Los resultados lo han confirmado ya que, con esta configuración, en 275 episodios se ha obtenido un agente entrenado