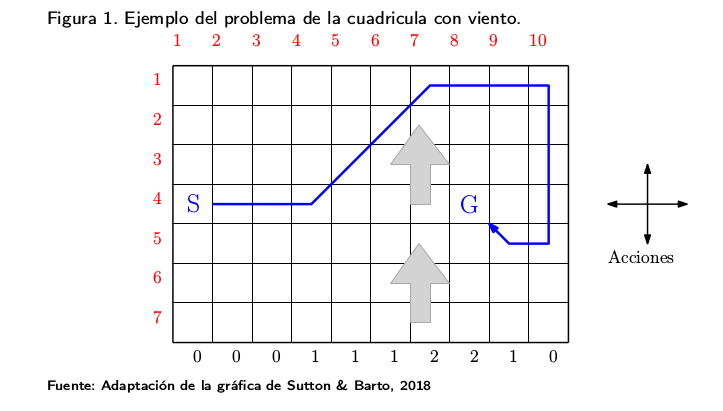
0. El entorno WindyGridWorld
El entorno WindyGridWorld consiste en un agente que se mueve en una cuadrícula 7x10 (alto x ancho). En cada paso, el agente tiene 4 opciones de acción o movimiento: ARRIBA, ABAJO, DERECHA, IZQUIERDA. El agente siempre sale de la misma casilla [3, 0] y el juego termina cuando el agente llega a la casilla de llegada [3, 7].
El entorno se corresponde con el ejemplo 'Cuadrícula con viento' explicado en la sección 3.1.2. el módulo "Métodos de Diferencia Temporal". El problema radica en que hay un viento que empuja al agente hacia arriba en la parte central de la cuadrícula. Esto provoca que, aunque se ejecute una acción estándar, en la región central los estados resultantes se desplazan hacia arriba por un viento cuya fuerza varía entre columnas.
El código para implementar este entorno, que se encuentra disponible en el fichero adjunto windy_gridworld_env.py, ha sido adaptado del siguiente enlace:
Vamos a empezar cargando el entorno y ver qué características tiene, ejecutando un episodio de prueba.
0.1. Carga de datos
El siguiente código carga los paquetes necesarios para el ejemplo, crea el entorno mediante la instanciación de un objeto de la clase WindyGridworldEnv (importada del archivo adjunto windy_gridworld_env.py) e imprime por pantalla la dimensión del espacio de acciones (0=arriba, 1=derecha, 2=abajo y 3=izquierda), el espacio de observaciones (una tupla que indica la posición del agente en la cuadrícula) y el rango de la variable de recompensa (cuyo valor es -1 para cualquier acción y que por tanto va de menos infinito a más infinito).
!pip install gym
import gym
import numpy as np
import windy_gridworld_env as wge
from collections import defaultdict
import sys
env=wge.WindyGridworldEnv()
print("Action space is {
} ".format(env.action_space))
print("Observation space is {} ".format(env.observation_space))
print("Reward range is {
} ".format(env.reward_range))
# Inicializamos el entorno
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
switch_action = {
0: "U",
1: "R",
2: "D",
3: "L",
}
while not done:
# Elegir una acción aleatoria (ésta es la implementación del agente)
action = env.action_space.sample()
# Ejecutar la acción y esperar la respuesta del entorno
new_obs, reward, done, info = env.step(action)
# Imprimir time-step
print("Action: {
} -> Obs: {} and reward: {}".format(switch_action[action], new_obs, reward))
# Actualizar variables
obs = new_obs
total_reward += reward
t += 1
print("Episode finished after {} timesteps and reward was {
} ".format(t, total_reward))
env.close()
1. Modificación del entorno
El entorno WindyGridWorld tiene varios parámetros que pueden ser modificados:
- La dimensión de la cuadrícula.
- La posición y fuerza del viento.
- La posición de las casillas de salida y de llegada.
Modificar el codigo de WindyGridWorld (fichero adjunto windy_gridworld_env.py) para que represente las propiedades de la cuadrícula descritas a continuación.
- Cuadrícula 15x15
- Fuerza del viento = [0, 0, 0, 1, 1, 1, 2, 2, 2, 1, 1, 1, 0, 0, 0]
- Casilla de inicio [8,0]
- Casilla final [8,7]
Guardar el entorno modificado en el archivo windy_gridworld_env_v2.py, en la misma carpeta que el original.
import gym
import numpy as np
import windy_gridworld_env_v2 as wge
env=wge.WindyGridworldEnv()
print("Action space is {
} ".format(env.action_space))
print("Observation space is {} ".format(env.observation_space))
print("Reward range is {
} ".format(env.reward_range))
print("Obs inicial: {
} ".format(obs))
A continuación, implementar un agente que siempre realice la misma acción: ir hacia la derecha y modificar el código para que sólo realice 10 time-steps.
Mostrar la trayectoria seguida por el agente. No es necesario graficarla, tan sólo mostrar las coordenadas de las casillas visitadas en orden.
# Environment reset
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
switch_action = {
0: "U",
1: "R",
2: "D",
3: "L"
}
def print_mapa(Movimientos, height, width):
print("")
print("")
print("Mapa:")
print("")
contador=0
for fila in range(0,height):
print('--------------------------------------------------------------\n', end="")
resultado= []
for columna in range(0,width):
#print(np.where(Q[fila,columna] == max(Q[fila,columna])))
coordenada = (fila, columna)
if coordenada in Movimientos.keys():
if Movimientos[coordenada]== 0:
resultado.append(' | U' )
if Movimientos[coordenada]== 1:
resultado.append(' | R' )
if Movimientos[coordenada]== 2:
resultado.append(' | D' )
if Movimientos[coordenada]== 3:
resultado.append(' | L')
if Movimientos[coordenada]== 4:
resultado.append(' | G')
else:
resultado.append(' | ')
print(''.join(resultado)+' |\n',end="")
print('--------------------------------------------------------------\n', end="")
# Escribir el código aquí
# Inicializamos el entorno
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
switch_action = {
0: "U",
1: "R",
2: "D",
3: "L",
}
Movimientos = defaultdict(lambda: np.zeros(env.action_space.n))
while not done and t<10:
print('Acción número ' + str(t+1))
# Elegir una acción aleatoria (ésta es la implementación del agente)
action = 1
# Ejecutar la acción y esperar la respuesta del entorno
new_obs, reward, done, info = env.step(action)
# Imprimir time-step
print("Action: {
} -> Obs: {} and reward: {}".format(switch_action[action], new_obs, reward))
Movimientos[obs]= action
# Actualizar variables
obs = new_obs
total_reward += reward
t += 1
print("Episode finished after {} timesteps and reward was {
} ".format(t, total_reward))
env.close()
print("A continucación muestro el movimiento del agente para validar la implementación del ejercio.");
print_mapa(Movimientos, 15, 15)
2. Métodos de Montecarlo
Dado que el entorno es determinista, es factible encontrar una política óptima (que puede no ser única) que consiga el mayor retorno (y por tanto la trayectoria más corta).
El objetivo de este apartado es realizar una estimación de la política óptima mediante los métodos de Montecarlo, en concreto estudiaremos el algoritmo On-policy first-visit MC control (para políticas $\epsilon$-soft).
Implementar el Algoritmo 3 explicado en el módulo "Métodos de Montecarlo" utilizando los siguientes parámetros:
- Número de episodios = 250000
- Epsilon = 0.1
- Factor de descuento = 1
def make_epsilon_greedy_policy(Q, epsilon, nA):
"""
Creates an epsilon-greedy policy based on a given Q-function and epsilon.
Args:
Q: A dictionary that maps from state -> action-values.
Each value is a numpy array of length nA (see below)
epsilon: The probability to select a random action . float between 0 and 1.
nA: Number of actions in the environment.
Returns:
A function that takes the observation as an argument and returns
the probabilities for each action in the form of a numpy array of length nA.
"""
def policy_fn(observation):
A = np.ones(nA, dtype=float) * epsilon / nA
best_action = np.argmax(Q[observation])
A[best_action] += (1.0 - epsilon)
return A
return policy_fn
def mc_control_epsilon_greedy(env, num_episodes, discount_factor=1.0, epsilon=0.1):
"""
Monte Carlo Control using Epsilon-Greedy policies.
Finds an optimal epsilon-greedy policy.
Args:
env: OpenAI gym environment.
num_episodes: Number of episodes to sample.
discount_factor: Gamma discount factor.
epsilon: Chance the sample a random action. Float betwen 0 and 1.
Returns:
A tuple (Q, policy).
Q is a dictionary mapping state -> action values.
policy is a function that takes an observation as an argument and returns
action probabilities
"""
# Keeps track of sum and count of returns for each state
# to calculate an average. We could use an array to save all
# returns (like in the book) but that's memory inefficient.
returns_sum = defaultdict(float)
returns_count = defaultdict(float)
# The final action-value function.
# A nested dictionary that maps state -> (action -> action-value).
Q = defaultdict(lambda: np.zeros(env.action_space.n))
# The policy we're following
policy = make_epsilon_greedy_policy(Q, epsilon, env.action_space.n)
for i_episode in range(1, num_episodes + 1):
# Print out which episode we're on, useful for debugging.
if i_episode % 100 == 0:
print("\rEpisode {}/{
}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# Generate an episode.
# An episode is an array of (state, action, reward) tuples
episode = []
state = env.reset()
#for t in range(1000000): #si es hasta que done se hace eterno
for t in range(1000): #considero que este es el mejor limite
#while True:
probs = policy(state)
action = np.random.choice(np.arange(len(probs)), p=probs)
next_state, reward, done, _ = env.step(action)
episode.append((state, action, reward))
if done:
break
state = next_state
# Find all (state, action) pairs we've visited in this episode
# We convert each state to a tuple so that we can use it as a dict key
sa_in_episode = set([(tuple(x[0]), x[1]) for x in episode])
for state, action in sa_in_episode:
sa_pair = (state, action)
# Find the first occurance of the (state, action) pair in the episode
first_occurence_idx = next(i for i,x in enumerate(episode)
if x[0] == state and x[1] == action)
# Sum up all rewards since the first occurance
G = sum([x[2]*(discount_factor**i) for i,x in enumerate(episode[first_occurence_idx:])])
# Calculate average return for this state over all sampled episodes
returns_sum[sa_pair] += G
returns_count[sa_pair] += 1.0
Q[state][action] = returns_sum[sa_pair] / returns_count[sa_pair]
# The policy is improved implicitly by changing the Q dictionary
return Q, policy
# Environment reset
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
Q, policy = mc_control_epsilon_greedy(env, num_episodes=250000, epsilon=0.1,discount_factor=1.0)
# Environment reset
obs = env.reset()
t, total_reward, done = 0, 0, False
state = env.reset()
episode = []
print("Ruta óptima")
while True:
probs = policy(state)
action = np.argmax(probs)
next_state, reward, done, info = env.step(action)
print("Action: {
} -> Obs: {} and reward: {}".format(action, next_state, reward))
episode.append((state, action, reward))
if done:
break
state = next_state
Implementar una función que imprima por pantalla la política óptima encontrada para cada celda.
Se muestra a continuación una imagen de ejemplo para la cuadrícula del entorno modificado de 15x15.

import sys
def print_all(policy, height, width):
obs = env.reset()
t, total_reward, done = 0, 0, False
state = env.reset()
episode = []
Movimientos = defaultdict(lambda: np.zeros(env.action_space.n))
print("Movimientos:")
print("")
for fila in range(0,15):
for columna in range(0,15):
state = (fila, columna)
probs = policy(state)
action = np.argmax(probs)
next_state, reward, done, info = env.step(action)
Movimientos[state]= action
#print(state+ '\n' , end="")
state = next_state
# Escribir el código aquí
#print(Movimientos.keys()
print_mapa(Movimientos, height, width)
def print_policy(policy, height, width):
obs = env.reset()
t, total_reward, done = 0, 0, False
state = env.reset()
episode = []
Movimientos = defaultdict(lambda: np.zeros(env.action_space.n))
print("Movimientos:")
print("")
reward_final = 0;
movimientos_realizados = 0;
while True:
probs = policy(state)
action = np.argmax(probs)
next_state, reward, done, info = env.step(action)
print("Action: {
} -> Obs: {} and reward: {} \n".format(action, next_state, reward), end="")
sys.stdout.flush()
episode.append((state, action, reward))
Movimientos[state]= action
#print(state+ '\n' , end="")
reward_final=reward_final+reward
movimientos_realizados = movimientos_realizados +1
if movimientos_realizados>50 and state in Movimientos.keys():
sys.stdout.flush()
print('Posible bucle en la Solución- Considero que la solución no va a ser valida.')
print('Para evitar bucles infinitos en las soluciones con un nivel bajo de episodios añado esta condición')
break;
if movimientos_realizados>12 and state == next_state:
sys.stdout.flush()
print('Bucle en la solucion- Con este metodo no se ha encontrado una solucion valida.')
break;
'''
probs = np.delete(probs,np.argmax(probs))
action = np.argmax(probs)
next_state, reward, done, info = env.step(action)
print("Action: {} -> Obs: {} and reward: {} \n".format(action, next_state, reward), end="")
sys.stdout.flush()
episode.append((state, action, reward))
Movimientos[state]= action
'''
else:
state = next_state
sys.stdout.flush()
if done:
print('La recompensa final es: ' + str(reward_final) + " ; además se han realizado "+ str(movimientos_realizados) + " Movimientos")
Movimientos[state]= 4
break
# Escribir el código aquí
#print(Movimientos.keys())
print_mapa(Movimientos, height, width)
def print_mapa(Movimientos, height, width):
print("")
print("")
print("Mapa:")
print("")
contador=0
for fila in range(0,height):
print('--------------------------------------------------------------\n', end="")
resultado= []
for columna in range(0,width):
#print(np.where(Q[fila,columna] == max(Q[fila,columna])))
coordenada = (fila, columna)
if coordenada in Movimientos.keys():
if Movimientos[coordenada]== 0:
resultado.append(' | U' )
if Movimientos[coordenada]== 1:
resultado.append(' | R' )
if Movimientos[coordenada]== 2:
resultado.append(' | D' )
if Movimientos[coordenada]== 3:
resultado.append(' | L')
if Movimientos[coordenada]== 4:
resultado.append(' | G')
else:
resultado.append(' | ')
print(''.join(resultado)+' |\n',end="")
print('--------------------------------------------------------------\n', end="")
print_policy(policy,15,15)
print_all(policy,15,15)
Ejecutar un episodio con la política óptima encontrada y mostrar la trayectoria del agente y el retorno obtenido.
print_policy(policy,15,15)
Implementar el algoritmo de Q-learning explicado en el modulo "Aprendizaje por Diferencia Temporal" utilizando los siguientes parámetros (1 punto):
- Número de episodios = 200
- learning rate = 0.5
- discount factor = 1
- epsilon = 0.05
Además, se pide:
- Mostrar por pantalla los valores Q estimados para cada estado.
- Mostrar por pantalla los valores de la función de valor $v_\pi(s)$ estimada para cada estado.
- Ejecutar un episodio siguiendo la política óptima encontrada, donde se pueda reconocer la trayectoria seguida por el agente.
import numpy as np
import pandas as pd
import itertools
def createEpsilonGreedyPolicy(Q, epsilon, num_actions):
"""
Creates an epsilon-greedy policy based
on a given Q-function and epsilon.
Returns a function that takes the state
as an input and returns the probabilities
for each action in the form of a numpy array
of length of the action space(set of possible actions).
"""
def policyFunction(state):
Action_probabilities = np.ones(num_actions,
dtype = float) * epsilon / num_actions
best_action = np.argmax(Q[state])
Action_probabilities[best_action] += (1.0 - epsilon)
return Action_probabilities
return policyFunction
def qLearning(env, num_episodes, discount_factor = 1.0,
alpha = 0.5, epsilon = 0.05):
"""
Q-Learning algorithm: Off-policy TD control.
Finds the optimal greedy policy while improving
following an epsilon-greedy policy"""
# Action value function
# A nested dictionary that maps
# state -> (action -> action-value).
Q = defaultdict(lambda: np.zeros(env.action_space.n))
# Create an epsilon greedy policy function
# appropriately for environment action space
policy = createEpsilonGreedyPolicy(Q, epsilon, env.action_space.n)
# For every episode
for ith_episode in range(num_episodes):
# Reset the environment and pick the first action
state = env.reset()
for t in itertools.count():
# get probabilities of all actions from current state
action_probabilities = policy(state)
# choose action according to
# the probability distribution
action = np.random.choice(np.arange(
len(action_probabilities)),
p = action_probabilities)
# take action and get reward, transit to next state
next_state, reward, done, _ = env.step(action)
# TD Update
best_next_action = np.argmax(Q[next_state])
td_target = reward + discount_factor * Q[next_state][best_next_action]
td_delta = td_target - Q[state][action]
Q[state][action] += alpha * td_delta
# done is True if episode terminated
if done:
break
state = next_state
return Q,policy
Q,policy = qLearning(env, 1000)
for fila in range(0,15):
print('--------------------------------------------------------------')
resultado= []
for columna in range(0,15):
#print(np.where(Q[fila,columna] == max(Q[fila,columna])))
#resultado.append(' |'+str(Q[fila,columna]) )
print("Para la fila {} y la columna {} tenemos el siguiente estado Q {} ".format(fila,columna,Q[fila,columna]))
#print(''.join(resultado)+' |')
print('--------------------------------------------------------------')
print_policy(policy,15,15)
print_all(policy, 15, 15)
4. Comparativa de los algoritmos
En este apartado haremos diferentes comparativas de las implementaciones de los metodos de Montecarlo y los metodos de Diferencia Temporal implementados anteriormente.
Compararemos el comportamiento de los dos algoritmos al modificar los valores del factor de descuento, el learning rate y el numero de episodios.
Para cada ejercicio se debe mostrar y justificar el resultado.
NOTA: se recomienda realizar varias veces las simulaciones en cada ejercicio, ya que éstas son aleatorias, y comentar el resultado más frecuente.
Analizar la búsqueda de la política óptima (convergencia al valor óptimo) ejecutando el algoritmo de Montecarlo al variar el número de episodios. En particular, se pide ejecutar el algoritmo para un número de episodios igual a 1000, 10000, 50000, 100000 y 200000, y describir los cambios en términos de la política encontrada para cada simulación, así como el número de pasos para alcanzar la casilla de llegada.
# Escribir el código de las simulaciones aquí
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
test = [ 1000 , 10000, 50000, 100000 , 200000]
for episodes in test:
obs = env.reset()
t, total_reward, done = 0, 0, False
Q, policy = mc_control_epsilon_greedy(env, num_episodes=episodes, epsilon=0.1)
print('------------------------------------------------------')
print('Conclusión de la política '+ str(episodes))
print_policy(policy,15,15)
CONCLUSIONES:
El resultado que he obtenido con el algoritmo de Montecarlo ha sido la siguiente tabla:
| 1000 | 10000 | 50000 | 100000 | 200000 |
|---|---|---|---|---|
| Fallido | -12 | -18 | -16 | -14 |
Como se puede observar, el algoritmo de Montecarlo tiene cierto nivel de aleatoriedad. Esto significa que cuando más episodios realizamos más posibilidades tienes para encontrar la ruta óptima y, por lo tanto, de entrenar nuestra política para obtener un mejor resultado.
Dicho esto, en la iteración con 1000 episodios no hemos obtenido una política válida para encontrar el objetivo. Posteriormente, en las diferentes iteraciones superiores sí que hemos conseguido obtener una política válida.
Mi conclusión a esta observación es que, con esta configuración, el número de episodios afecta en la probabilidad de éxito para obtener la mejor política.
Y este matiz de probabilidad lo hemos encontrado en la segunda iteración del algoritmo, donde con una implementación de 10000 episodios de entrenamiento hemos conseguido obtener una política capaz de obtener la recompensa de la forma más óptima que la implementación con 200000 episodios. Ahora bien, los resultados muestran como a una mayor cantidad de episodios utilizada tendremos más probabilidades de implementar una política más certera.
Analizar la búsqueda de la política óptima ejecutando el algoritmo Q-learning al variar el número de episodios. En particular, se pide ejecutar el algoritmo para un número de episodios igual a 10000, 1000, 500, 100 y 50, y describir los cambios en términos de la función de valor, así como el número de pasos para alcanzar la casilla de llegada. Comentar las diferencias más significativas respecto al apartado anterior.
def createEpsilonGreedyPolicy(Q, epsilon, num_actions):
"""
Creates an epsilon-greedy policy based
on a given Q-function and epsilon.
Returns a function that takes the state
as an input and returns the probabilities
for each action in the form of a numpy array
of length of the action space(set of possible actions).
"""
def policyFunction(state):
Action_probabilities = np.ones(num_actions,
dtype = float) * epsilon / num_actions
best_action = np.argmax(Q[state])
Action_probabilities[best_action] += (1.0 - epsilon)
return Action_probabilities
return policyFunction
def qLearning(env, num_episodes, discount_factor = 1.0,
alpha = 0.5, epsilon = 0.05):
"""
Q-Learning algorithm: Off-policy TD control.
Finds the optimal greedy policy while improving
following an epsilon-greedy policy"""
# Action value function
# A nested dictionary that maps
# state -> (action -> action-value).
Q = defaultdict(lambda: np.zeros(env.action_space.n))
# Create an epsilon greedy policy function
# appropriately for environment action space
policy = createEpsilonGreedyPolicy(Q, epsilon, env.action_space.n)
steps = []
# For every episode
for ith_episode in range(num_episodes):
# Reset the environment and pick the first action
state = env.reset()
for t in itertools.count():
# get probabilities of all actions from current state
action_probabilities = policy(state)
# choose action according to
# the probability distribution
action = np.random.choice(np.arange(
len(action_probabilities)),
p = action_probabilities)
# take action and get reward, transit to next state
next_state, reward, done, _ = env.step(action)
# TD Update
best_next_action = np.argmax(Q[next_state])
td_target = reward + discount_factor * Q[next_state][best_next_action]
td_delta = td_target - Q[state][action]
Q[state][action] += alpha * td_delta
# done is True if episode terminated
if done:
steps.append(t)
break
state = next_state
return Q,policy,steps
# Escribir el código de las simulaciones aquí
from pylab import *
# importar el módulo pyplot
import matplotlib.pyplot as plt
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
test = [ 10000, 1000, 500, 100 , 50]
for episodes in test:
obs = env.reset()
t, total_reward, done = 0, 0, False
Q, policy, steps= qLearning(env, episodes)
print('------------------------------------------------------')
print('Conclusión de la política '+ str(episodes))
print_policy(policy,15,15)
# importar todas las funciones de pylab
print('Gráfica con la evolución de los steps a lo largo de los episodios')
plot(steps)
show()
print('Mediana:' + str(median(steps)))
print('Media:' + str(mean(steps)))
El resultado que he obtenido con Q-learning ha sido el siguiente:
| 10000 | 1000 | 500 | 100 | 50 |
|---|---|---|---|---|
| -12 | -12 | -12 | -12 | Fallida |
CONCLUSIONES: Realmente con este algoritmo he obtenido una política óptima en tan solo 100 episodios. Estos resultados confirman que Q-learning es capaz de obtener mejores resultados que el algoritmo Montecarlo en un entorno sin aleatoriedad como el que nos encontramos en este juego.
Dicho esto, este algoritmo aprende antes de ver el resultado final, debido a que puede estimar cual será el retorno de una situación dado el punto en donde se encuentra, esto quiere decir que TD puede ir aprendiendo durante cada paso dentro del camino.
También se observa que este algoritmo converge muy rápidamente y es capaz de obtener la política óptima en muy pocos episodios.
Ejecutar el algoritmo de Montecarlo y el algoritmo Q-learning con discount factor=0.1 y el resto de parámetros iguales que en los ejercicios 2 y 3. Describir los cambios en la política óptima, comparando el resultado obtenido con el resultado de los ejercicios 2 y 3 (discount factor=1).
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
obs = env.reset()
t, total_reward, done = 0, 0, False
Q, policy = mc_control_epsilon_greedy(env, num_episodes=250000,discount_factor=0.1, epsilon=0.1)
print('------------------------------------------------------')
print('Conclusión de la política '+ str(250000))
print_policy(policy,15,15)
# Escribir el código de las simulaciones aquí
# Escribir el código de las simulaciones aquí
# Escribir el código de las simulaciones aquí
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
obs = env.reset()
t, total_reward, done = 0, 0, False
Q, policy = mc_control_epsilon_greedy(env, num_episodes=250000,discount_factor=0.1, epsilon=0.1)
print('------------------------------------------------------')
print('Conclusión de la política '+ str(250000))
print_policy(policy,15,15)
def createEpsilonGreedyPolicy(Q, epsilon, num_actions):
"""
Creates an epsilon-greedy policy based
on a given Q-function and epsilon.
Returns a function that takes the state
as an input and returns the probabilities
for each action in the form of a numpy array
of length of the action space(set of possible actions).
"""
def policyFunction(state):
Action_probabilities = np.ones(num_actions,
dtype = float) * epsilon / num_actions
best_action = np.argmax(Q[state])
Action_probabilities[best_action] += (1.0 - epsilon)
return Action_probabilities
return policyFunction
def qLearning(env, num_episodes, discount_factor = 1.0,
alpha = 0.5, epsilon = 0.05):
"""
Q-Learning algorithm: Off-policy TD control.
Finds the optimal greedy policy while improving
following an epsilon-greedy policy"""
# Action value function
# A nested dictionary that maps
# state -> (action -> action-value).
Q = defaultdict(lambda: np.zeros(env.action_space.n))
# Create an epsilon greedy policy function
# appropriately for environment action space
policy = createEpsilonGreedyPolicy(Q, epsilon, env.action_space.n)
steps = []
# For every episode
for ith_episode in range(num_episodes):
# Reset the environment and pick the first action
state = env.reset()
for t in itertools.count():
# get probabilities of all actions from current state
action_probabilities = policy(state)
# choose action according to
# the probability distribution
action = np.random.choice(np.arange(
len(action_probabilities)),
p = action_probabilities)
# take action and get reward, transit to next state
next_state, reward, done, _ = env.step(action)
# TD Update
best_next_action = np.argmax(Q[next_state])
td_target = reward + discount_factor * Q[next_state][best_next_action]
td_delta = td_target - Q[state][action]
Q[state][action] += alpha * td_delta
# done is True if episode terminated
if done:
steps.append(t)
break
state = next_state
return Q,policy,steps
# Escribir el código de las simulaciones aquí
# Escribir el código de las simulaciones aquí
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
obs = env.reset()
t, total_reward, done = 0, 0, False
Q, policy,steps = qLearning(env, 1000,discount_factor=0.1)
print('------------------------------------------------------')
print('Conclusión de la política '+ str(1000))
print_policy(policy,15,15)
from pylab import *
import matplotlib.pyplot as plt
print('Gráfica con la evolución de los steps a lo largo de los episodios')
plot(steps)
show()
print('Mediana:' + str(median(steps)))
print('Media:' + str(mean(steps)))
Q,policy,steps = qLearning(env, 1000)
# importar todas las funciones de pylab
from pylab import *
# importar el módulo pyplot
import matplotlib.pyplot as plt
print('Gráfica con la evolución de los steps a lo largo de los episodios')
plot(steps)
show()
print('Mediana:' + str(median(steps)))
print('Media:' + str(mean(steps)))
CONCLUSIONES:
Si recordamos la teoría, el factor de descuento determina la importancia de recompensas futuras. Un factor de 0 hará que el agente sea "miope" (o corto de miras) por considerar únicamente las recompensas a corto plazo, mientras que un factor que se acerca a 1 hará que luche por una recompensa alta a largo plazo.
En el algoritmo de monte carlo no hemos pasado de las primeras casillas ya que con esta configuración no se prima la investigación. El factor de descuento se introduce para evitar que los problemas continuos manejen recompensas infinitas pero en un entorno tan limitado no son buenas ya que se ha primado los movimientos iniciales sobre los más alejados y, por lo tanto, las recompensas para los movimientos acertados no se diferencian lo suficiente con los aciertos. Por este motivo no es una solución óptima.
Respecto a Q-learning no he encontrado ninguna merma en el algoritmo en la cantidad de recompensas obtenida. Lo que sí que he observado es que disminuye bastante la media de los episodios si utilizamos discount factor = 1 y, en cambio, aumenta cuando tenemos un discount factor = 0.1. Entiendo que el algoritmo realiza más iteraciones y busca más soluciones en cada iteración que permitan resolver el juego ya que la merma de las recompensas con un discount factor = 0.1. provoca una pérdida de la capacidad de discernir entre las diferentes soluciones. Las recompensas han disminuido tanto que todas las soluciones tienen una recompensa muy pareja.
Ejecutar el algoritmo de Q-learning con los siguientes valores de learning rate: 0.1 y 0.9. Analizar las diferencias con los resultados obtenidos en la pregunta 3 en términos de número de time-steps para llegar a la posición objetivo. Para ello, es necesario usar el mismo número de episodios. Finalmente, comparar el número de pasos por episodio (representar gráficamente el número de time-steps para cada episodio de la simulación en ambos casos) y verificar con que valor de learning rate el algoritmo converge más rápidamente.
# Escribir el código de las simulaciones aquí
# Escribir el código de las simulaciones aquí
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
obs = env.reset()
t, total_reward, done = 0, 0, False
Q, policy, steps = qLearning(env, 1000, alpha = 0.1 )
print('------------------------------------------------------')
print('Conclusión de la política '+ str(250000))
print_policy(policy,15,15)
# importar todas las funciones de pylab
from pylab import *
# importar el módulo pyplot
import matplotlib.pyplot as plt
print('Gráfica con la evolución de los steps a lo largo de los episodios')
plot(steps)
show()
print('Mediana:' + str(median(steps)))
print('Media:' + str(mean(steps)))
# Escribir el código de las simulaciones aquí
# Escribir el código de las simulaciones aquí
obs = env.reset()
t, total_reward, done = 0, 0, False
print("Obs inicial: {
} ".format(obs))
obs = env.reset()
t, total_reward, done = 0, 0, False
Q, policy, steps= qLearning(env, 1000, alpha = 0.9 )
print('------------------------------------------------------')
print('Conclusión de la política '+ str(250000))
print_policy(policy,15,15)
# importar todas las funciones de pylab
from pylab import *
# importar el módulo pyplot
import matplotlib.pyplot as plt
print('Gráfica con la evolución de los steps a lo largo de los episodios')
plot(steps)
show()
print('Mediana:' + str(median(steps)))
print('Media:' + str(mean(steps)))
CONCLUSIONES:
Cómo puedo comprobar en las gráficas con la cantidad de pasos, al aumentar el valor de alpha disminuyen la cantidad de pasos en el algoritmo. Es decir, hemos obtenido una solución más óptima más rápidamente.
Alpha determina hasta qué punto la información adquirida sobrescribe la información vieja. Un factor de 0 hace que el agente no aprende (únicamente aprovechando el conocimiento previo), mientras un factor de 1 hace que el agente considere sólo la información más reciente (ignorando el conocimiento previo para explorar posibilidades).
En entornos totalmente deterministas cómo el juego analizado, un índice de aprendizaje de alpha=1 es óptimo. Cuándo el problema es estocástico, el algoritmo converge bajo determinadas condiciones técnicas en el índice de aprendizaje que requiere un descenso hasta cero. Esto es debido a que el escenario es el mismo y no es necesario reescribir lo aprendido.